题目 对于定义在区间 $D$ 上的函数 $f\left( x \right)$ 和 $g\left( x \right)$，如果对于任意 $x \in D$，都有 $\left| {f\left( x \right) - g\left( x \right)} \right| \leqslant 1$ 成立，那么称函数 $f\left( x \right)$ 在区间 $D$ 上可被函数 $g\left( x \right)$ 替代． 问题1 若函数 $f\left( x \right) = x$，$g\left( x \right) = 1 - \dfrac{1}{{4x}}$，试判断在区间 $\left[ {\dfrac{1}{4}, \dfrac{3}{2}} \right]$ 上 $f\left( x \right)$ 能否被 $g\left( x \right)$ 替代； 答案1 能 解析1 函数 $f\left( x \right)$ 在区间 $D$ 上可被函数 $g\left( x \right)$ 替代的充要条件是$$\forall x \in D , f\left( x \right) - 1 \leqslant g\left( x \right) \leqslant f\left( x \right) + 1,$$只需考虑$$\forall x \in \left[ {\dfrac{1}{4}, \dfrac{3}{2}} \right],x - 1 \leqslant 1 - \dfrac{1}{{4x}} \leqslant x + 1$$的正确性．<br/>用分析法，上式等价于$$\forall x \in \left[ {\dfrac{1}{4}, \dfrac{3}{2}} \right] , 4{x^2} - 8x + 1 \leqslant 0\land 4{x^2} + 1 \geqslant 0,$$整理得$$ \forall x \in \left[ {\dfrac{1}{4}, \dfrac{3}{2}} \right], 4{\left( {x - 1} \right)^2} \leqslant 3,$$上式恒成立，因此，在区间 $\left[ {\dfrac{1}{4}, \dfrac{3}{2}} \right]$ 上 $f\left( x \right)$ 能被 $g\left( x \right)$ 替代． 备注1 问题2 若函数 $f\left( x \right) = \ln \left( {a{x^2} + x} \right)$（$x \in {D_1}$），$g\left( x \right) = \sin x$（$x \in {D_2}$），问是否存在常数 $a$，使得 $f\left( x \right)$ 在 ${D_1} \cap {D_2}$ 上能被 $g\left( x \right)$ 替代？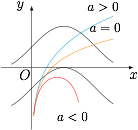若存在，则求出 $a$ 的取值范围；若不存在，请说明理由． 答案2 不存在 解析2 考虑$$\sin x - 1 \leqslant \ln \left( {a{x^2} + x} \right) \leqslant \sin x + 1,$$如图，<img src="/static/images/1e18bcabfef7aa5a4469b3a5ebf557d0.png" class="img-responsive" /><case>情形一</case>当 $a \geqslant 0$ 时，若 $x>0$ 且 $x\to 0$，则 $\ln(ax^2+x)\to-\infty$，而 $\sin x-1\geqslant -2$，所以 $f\left( x \right)$ 不能在定义域上被 $g\left( x \right)$ 代替；<br/><case>情形二</case>当 $a < 0$ 时，$f\left( x \right)$ 的定义域为 $\left( {0, - \dfrac{1}{a}} \right)$，在 $\left( {0, - \dfrac{1}{{2a}}} \right)$ 上单调递增，同样地，当 $x>0,x\to 0$ 时，有 $\ln(ax^2+x)\to -\infty$，所以 $f(x)$ 不能被 $g(x)$ 代替．<br/>综上知，$a$ 不存在． 备注2