题目 已知点 $P\left( {0, - \dfrac{3}{2}} \right)$，点 $A$ 在 $x$ 轴上，点 $B$ 在 $y$ 轴的正半轴上，点 $M$ 在直线 $AB$ 上，且满足 $\overrightarrow {PA} \cdot \overrightarrow {AB} = 0$，$\overrightarrow {AM} = 3\overrightarrow {AB} $． 问题1 当点 $A$ 在 $x$ 轴上移动时，求动点 $M$ 的轨迹 $C$ 的方程； 答案1 ${x^2} = 2y$（$y > 0$） 解析1 设 $A\left( {{x_1}, 0} \right),B\left( {0, {y_1}} \right),M\left( {x, y} \right)$，则$$\left( {{x_1}, \dfrac{3}{2}} \right) \cdot \left( { - {x_1}, {y_1}} \right) = 0 , \left( {x - {x_1}, y} \right) = 3\left( { - {x_1}, {y_1}} \right),$$于是$$\begin{cases}<br/>\dfrac{3}{2}{y_1} = {x_1}^2,\\<br/>x = - 2{x_1},\\<br/>y = 3{y_1},\\<br/>\end{cases}$$消参可得$$\dfrac{3}{2} \cdot \dfrac{y}{3} = {\left( { - \dfrac{x}{2}} \right)^2},$$即 ${x^2} = 2y$（$y > 0$）． 备注1 问题2 设 $Q$ 为 $(1)$ 中的曲线 $C$ 上一点，直线 $l$ 过点 $Q$ 且与曲线 $C$ 在点 $Q$ 处的切线垂直，$l$ 与曲线 $C$ 相交于另一点 $R$，当 $\overrightarrow {OQ} \cdot \overrightarrow {OR} = 0$（$O$ 为坐标原点）时，求直线 $l$ 的方程． 答案2 $y = \pm \dfrac{{\sqrt 2 }}{2}x + 2$ 解析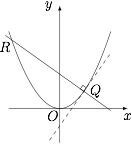2 如图．<img src="/static/images/0e21f125c4257ffc4ba3c0ed5c53a642.png" class="img-responsive" />设直线 $l$ 的方程为 $y = kx + b$，则联立直线 $l$ 与抛物线的方程，有$${x^2} = 2y \cdot \dfrac{{y - kx}}{b},$$由 $\overrightarrow {OQ} \perp \overrightarrow {OR} $ 有$$b = 2,$$设切点 $Q\left( {{x_0}, {y_0}} \right)$，则切线为$${x_0}x = y + {y_0},$$于是直线 $RQ$ 的方程为$$y = - \dfrac{1}{{{x_0}}}\left( {x - {x_0}} \right) + {y_0},$$与 $y = kx + 2$ 对比，有$$\begin{cases} k = - \dfrac{1}{{{x_0}}},\\2 = {y_0} + 1,\end{cases}$$而 $x_0^2 = 2{y_0}$，解得$${x_0} = \pm \sqrt 2,{y_0} = 1,k = \mp \dfrac{{\sqrt 2 }}{2},$$所以直线 $l$ 的方程为 $y = \pm \dfrac{{\sqrt 2 }}{2}x + 2$． 备注2