四面体 $ABCD$ 中，$AB=CD$，$AC=BD$，$AD=BC$．
【难度】
【出处】
2009年清华大学保送生试题（理科）
【标注】
-
求证：四面体每个面的三角形为锐角三角形；标注答案略解析根据题意，设$$AB=CD=x , AC=BD=y , AD=BC=z,$$如图．
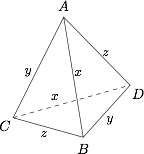因为$$ \triangle ABC\cong\triangle DCB\cong\triangle BAD\cong\triangle CAD ,$$且$$ \angle ACD+\angle ACB>\angle BCD$$（这是容易证明的），因此$$ \angle BAC+\angle ACB>\angle CBA.$$类似的，也有$$ \angle BAC+\angle CBA>\angle ACB,$$于是 $\triangle ABC$ 为锐角三角形，因此，四面体的每个面的三角形均为锐角三角形． -
设三个面与底面 $BCD$ 所成的角分别为 $\alpha ,\beta ,\gamma $，求证：$\cos \alpha +\cos \beta +\cos \gamma =1$．标注答案略解析作 $AO\perp $ 面 $BCD$ 于点 $O$，如图．
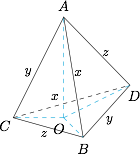根据射影定理，有$$\cos \alpha +\cos \beta +\cos \gamma =\dfrac{{{S}_{\triangle OBC}}}{{{S}_{\triangle ABC}}}+\dfrac{{{S}_{\triangle OBD}}}{{{S}_{\triangle ABD}}}+\dfrac{{{S}_{\triangle OCD}}}{{{S}_{\triangle ACD}}}=1.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
