设定义在 $ {\mathbb{R}} $ 上的函数 $ f\left(x\right) $ 是最小正周期为 $ 2{\mathrm \pi} $ 的偶函数,$ f '\left(x\right) $ 是 $ f\left(x\right) $ 的导函数.当 $ x\in \left[0,{\mathrm \pi} \right] $ 时,$ 0<f\left(x\right)<1 $;当 $ x\in \left(0,{\mathrm \pi} \right) $ 且 $ x\neq {\dfrac{\mathrm \pi} {2}} $ 时,$ \left(x-{\dfrac{{\mathrm \pi} }{2}} \right)f '\left(x\right)>0 $,则函数 $ y=f\left(x\right)-\sin x $ 在 $ \left[-2{\mathrm \pi} ,2{\mathrm \pi} \right] $ 上的零点个数为 \((\qquad)\)
【难度】
【出处】
2012年高考湖南卷(文)
【标注】
【答案】
B
【解析】
可根据条件作出函数 $ y=f \left(x \right) $ 与 $ y= \sin x $ 在 $ \left[-2{\mathrm \pi} ,2{\mathrm \pi} \right] $ 上的大致图象,利用两个函数图象的交点个数确定函数的零点个数.由条件可得 $ x\in \left(0,{\dfrac{\mathrm \pi} {2}} \right)$ 时 $ f '\left(x\right) <0$,$ f\left( x\right) $ 单调递减;$ x\in \left({\dfrac{\mathrm \pi} {2}} ,{\mathrm \pi} \right)$ 时,$ f '\left(x\right) >0$,$ f \left(x \right) $ 单调递增,又 $x\in\left(0,{\mathrm \pi} \right)$ 时,$ 0<f \left(x \right)<1 $,$ f \left(x\right) $ 是偶函数,所以可作出函数 $ y=f\left( x\right) $ 与 $ y=\sin x $ 在 $ \left[-2{\mathrm \pi} ,2{\mathrm \pi} \right] $ 上的大致图象,可知两个函数图象在 $ \left[-2{\mathrm \pi} ,2{\mathrm \pi} \right] $ 上共有 $ 4 $ 个交点.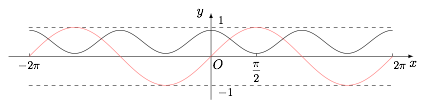

题目
答案
解析
备注