已知函数 $f(x)={\rm e}^{x}-{\rm e}x$.
【难度】
【出处】
无
【标注】
-
求函数 $f(x)$ 的最小值;标注答案$0$解析因为$$f'(x)={\rm e}^{x}-{\rm e},$$所以$$\min\left[f(x)\right]=f(1)=0.$$
-
求证:${\rm e}^{1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n-1}+\frac{1}{n}}>n+1(n\in\mathbb N^{*})$;标注答案略解析由 $(1)$,当 $x\ne 1$ 时,${\rm e}^{x}-{\rm e}x>0$,即$$x>\ln x+1.$$要证 ${\rm e}^{1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n-1}+\frac{1}{n}}>n+1$,就是要证\[1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n-1}+\dfrac{1}{n}>\ln (n+1).\]而\[\begin{split}1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n-1}+\dfrac{1}{n}&>\ln 2+\ln \dfrac{3}{2}+\cdots+\ln \dfrac{n+1}{n}\\ &=\ln (n+1),\end{split}\]所以原命题得证.
-
对于函数 $h(x)$ 与 $g(x)$ 定义域上的任意实数 $x$,若存在常数 $k,b$,使得 $h(x)\geqslant kx+b$ 和 $g(x)\leqslant kx+b$ 都成立,则称直线 $y=kx+b$ 为函数 $h(x)$ 与 $g(x)$ 的“分界线”.设函数 $h(x)=f(x)-{\rm e}^{x}+{\rm e}x+\dfrac{1}{2}x^{2}$,$g(x)={\rm e}\ln x$,$h(x)$ 与 $g(x)$ 是否存在“分界线”?若存在,求出 $k,b$ 的值;若不存在,请说明理由.标注答案存在;$k=\sqrt {\rm e}$,$b=-\dfrac{\rm e}{2}$解析由题意,$$h(x)=\dfrac{1}{2}x^{2} , g(x)={\rm e}\ln x.$$考查函数 $F(x)=h(x)-g(x)=\dfrac{1}{2}x^{2}-{\rm e}\ln x$,其导数为$$F'(x)=x-\dfrac{\rm e}{x},$$所以当 $x=\sqrt {\rm e}$ 时,$F(x)$ 取得最小值 $0$.
因此,经计算得 $h(x)$ 和 $g(x)$ 在 $\left(\sqrt{\rm e},\dfrac{\rm e}{2}\right)$ 处的切线方程为$$y=\sqrt{\rm e}x-\dfrac{\rm e}{2}.$$由于 $h'(x)=x$ 在 $(x\in(0,+\infty)$ 上单调递增,$g'(x)=\dfrac{\rm e}{x}$ 在 $x\in(0,+\infty)$ 上单调递减,因此\[\forall x\in(0,+\infty),h(x)\geqslant \sqrt{\rm e}x-\dfrac{\rm e}{2}\geqslant {\rm e}\ln x.\]从而 $h(x)$ 与 $g(x)$ 存在“分界线”$$y=\sqrt{\rm e}x-\dfrac{\rm e}{2},$$此时 $k$ 和 $b$ 的值分别为 $k=\sqrt {\rm e}$,$b=-\dfrac{\rm e}{2}$.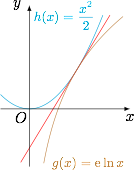
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3