如图，四边形 $ABCD$ 为圆 $O$ 的内接四边形，对边 $BC,AD$ 交于 $F$，$AB,DC$ 交于 $E$．$\triangle{ECF}$ 的外接圆与圆 $O$ 的另一交点为 $H$，$AH$ 交 $EF$ 于 $M$，$MC$ 交圆 $O$ 于 $G$．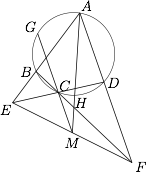
求证：
求证：【难度】
【出处】
2011年全国高中数学联赛辽宁省预赛
【标注】
-
$M$ 为 $EF$ 中点；标注答案略解析连结 $EH,CH,FH$，如图．
则有$$\angle{FAM}=\angle{DAH}=\angle{DCH}.$$由 $E,C,H,F$ 四点共圆，有$$\angle{DCH}=\angle{HFM},$$所以$$\angle{FAM}=\angle{HFM}.$$又因为 $\angle{HMF}=\angle{FMA}$，所以$$\triangle{HMF}\backsim \triangle{FMA},$$故有$$MF^2=MH\cdot MA.$$由 $E,C,H,F$ 四点共圆及 $A,B,C,H$ 四点共圆得$$\angle{HEM}=\angle{HEF}=\angle{HCF}=\angle{EAM}.$$又 $\angle{EMH}=\angle{AME}$，所以$$\triangle{EMH}\backsim \triangle{AME},$$从而$$ME^2=MH\cdot MA,$$所以 $MF^2=ME^2$，即 $MF=ME$．故 $M$ 为 $EF$ 中点． -
$A,G,E,F$ 四点共圆．标注答案略解析延长 $CM$ 到 $I$ 使 $MC=MI$，连接 $GA$．
因为$$ME=MF , MC=MI,$$所以四边形 $CEIF$ 为平行四边形，从而$$\angle{EIF}=\angle{ECF}=\angle{BCD},$$而 $\angle{BAD}+\angle{BCD}=180^{\circ}$，所以$$\angle{BAD}+\angle{EIF}=180^{\circ},$$因此 $A,E,I,F$ 四点共圆．
又因为$$\angle{GAE}=\angle{GAB}=\angle{GCB}=\angle{FCI}=\angle{EIC}=\angle{EIG},$$所以 $A,G,E,I$ 四点共圆．故 $A,G,E,I,F$ 五点共圆，从而 $A,G,E,F$ 四点共圆．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
