如图,$M$ 为 $\triangle{ABC}$ 的中线 $AD$ 的中点,过点 $M$ 的直线分别交两边 $AB,AC$ 于点 $P,Q$,设 $\overrightarrow{AP}=x\overrightarrow{AB}$,$\overrightarrow{AQ}=y\overrightarrow{AC}$,记 $y=f(x)$.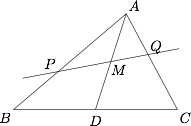

【难度】
【出处】
2011年全国高中数学联赛陕西省预赛二试
【标注】
-
求函数 $y=f(x)$ 的表达式;标注答案$f(x)=\dfrac x{4x-1},x\in\left[\dfrac 13,1\right]$解析因为过点 $M$ 的直线分别与两边 $AB$,$AC$ 相交,所以$$x>0 , y>0,$$从而$$\overrightarrow{AB}=\dfrac 1x \overrightarrow{AP},\overrightarrow{AC}=\dfrac 1y\overrightarrow{AQ}.$$于是\[\begin{split}\overrightarrow{AM}&=\dfrac 12 \overrightarrow{AD}\\&=\dfrac 14(\overrightarrow{AB}+\overrightarrow{AC})\\&=\dfrac 1{4x}\overrightarrow{AP}+\dfrac 1{4y}\overrightarrow{AQ}.\end{split}\]又 $P,M,Q$ 三点共线,所以$$\dfrac 1{4x}+\dfrac 1{4y}=1,$$即$$f(x)=y=\dfrac x{4x-1}.$$由 $0<y\leqslant 1$,得$$0<\dfrac{x}{4x-1}\leqslant 1,$$解得 $x\geqslant \dfrac 13$.
故 $y=f(x)=\dfrac x{4x-1},x\in\left[\dfrac 13,1\right]$. -
设 $g(x)=x^3+3ax^2+2a,x\in [0,1]$,若对任意 $x_1\in \left[\dfrac 13,1\right]$,总存在 $x_2\in [0,1]$,使得 $f(x_1)=g(x_2)$ 成立,求实数 $a$ 的取值范围.标注答案$\left(-\infty,-\dfrac 23\right]\cup\left[0,\dfrac 16\right]$解析因为$$g'(x)=3x^2+3a^2\geqslant 0,$$所以 $g(x)$ 在 $[0,1]$ 上是增函数,则$$\begin{split}g(x)_{\min}&=g(0)=2a,\\g(x)_{\max}&=g(1)=3a^2+2a+1,\end{split}$$即函数 $f(x)$ 的值域为 $[2a,3a^2+2a+1]$.
又$$f(x)=\dfrac x{4x-1}=\dfrac 14 +\dfrac{\dfrac 14}{4x-1}$$在 $\left[\dfrac 13,1\right]$ 上是减函数,所以$$\begin{split}f(x)_{\min}&=f(1)=\dfrac 13,\\f(x)_{\max}=f\left(\dfrac 13\right)=1,\end{split}$$即函数 $f(x)$ 的值域为 $\left[\dfrac 13,1\right]$.
由题设得$$\left[\dfrac 13,1\right]\subseteq [2a,3a^2+2a+1],$$则$$\begin{cases}2a\leqslant \dfrac 13,\\ 3a^2+2a+1\geqslant 1,\end{cases}$$解得 $a$ 的取值范围为 $\left(-\infty,-\dfrac 23\right]\cup\left[0,\dfrac 16\right]$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2