已知椭圆 $\dfrac{x^{2}}{4}+\dfrac{y^{2}}{3}=1$ 的内接平行四边形的一组对边分别过椭圆的焦点 $F_{1},F_{2}$，求该平行四边形面积的最大值．
【难度】
【出处】
2013年全国高中数学联赛山东省预赛
【标注】
【答案】
$6$
【解析】
由已知得$$|F_{1}F_{2}|=2.$$如图，椭圆的内接平行四边形 $ABCD$ 的一组对边 $BC,AD$ 分别过焦点 $F_{1}$ 和 $F_{2}$．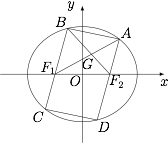
显然，线段 $BC,AD$ 以原点为中心对称，所以平行四边形 $ABCD$ 的对称中心为原点．
设点 $A$，$B$，$C$，$D$ 为坐标分别为 $A(x_{1},y_{1})$，$B(x_{2},y_{2})$，$C(x_{3},y_{3})$，$D(x_{4},y_{4})$，则\[\begin{split}S_{\text{平行四边形}ABCD}&=2\left(S_{\triangle BF_{1}F_{2}}+S_{\triangle ABF_{2}}\right)\\&=2\left(S_{\triangle BF_{1}F_{2}}+S_{\triangle AF_{1}F_{2}}\right)\\&=|F_{1}F_{2}|\cdot |y_{1}+y_{2}|\\&=2|y_{1}-y_{4}|.\end{split}\]若直线 $AD$ 的斜率存在，设其方程为 $y=k(x-1)$，代入椭圆方程得\[\dfrac{x^{2}}{4}+\dfrac{k^{2}(x-1)^{2}}{3}=1,\]整理得\[(3+4k^{2})x^{2}-8k^{2}x+4k^{2}-12=0,\]由韦达定理得\[x_{1}+x_{4}=\dfrac{8k^{2}}{3+4k^{2}},x_{1}x_{4}=\dfrac{4k^{2}-12}{3+4k^{2}},\]所以\[\begin{split}|y_{1}-y_{4}|^{2}&=k^{2}|x_{1}-x_{4}|^{2}\\&=k^{2}\left[(x_{1}+x_{4})^{2}-4x_{1}x_{4}\right]\\&=\dfrac{k^{2}}{(3+4k^{2})^{2}}\left[64k^{4}-16(3+4k^{2})(k^{2}-3)\right]\\&=9\cdot \dfrac{16k^{2}(k^{2}+1)}{(3+4k^{2})^{2}}.\end{split}\]故平行四边形 $ABCD$ 的面积为\[S_{\text{平行四边形}ABCD}=2|y_{1}-y_{4}|=6\sqrt{\dfrac{16k^{2}(1+k^{2})}{(3+4k^{2})^{2}}}<6.\]当 $AD$ 的斜率不存在，即 $AD$ 垂直于 $x$ 轴时，易得 $A\left(1,\dfrac{3}{2}\right)$，$D\left(1,-\dfrac{3}{2}\right)$，则$$|AD|=3 , d=|F_{1}F_{2}|=2,$$故\[S_{\text{平行四边形}ABCD}=|AD|\cdot d=6.\]综上所述，平行四边形 $ABCD$ 的面积最大值为 $6$．
显然，线段 $BC,AD$ 以原点为中心对称，所以平行四边形 $ABCD$ 的对称中心为原点．设点 $A$，$B$，$C$，$D$ 为坐标分别为 $A(x_{1},y_{1})$，$B(x_{2},y_{2})$，$C(x_{3},y_{3})$，$D(x_{4},y_{4})$，则\[\begin{split}S_{\text{平行四边形}ABCD}&=2\left(S_{\triangle BF_{1}F_{2}}+S_{\triangle ABF_{2}}\right)\\&=2\left(S_{\triangle BF_{1}F_{2}}+S_{\triangle AF_{1}F_{2}}\right)\\&=|F_{1}F_{2}|\cdot |y_{1}+y_{2}|\\&=2|y_{1}-y_{4}|.\end{split}\]若直线 $AD$ 的斜率存在，设其方程为 $y=k(x-1)$，代入椭圆方程得\[\dfrac{x^{2}}{4}+\dfrac{k^{2}(x-1)^{2}}{3}=1,\]整理得\[(3+4k^{2})x^{2}-8k^{2}x+4k^{2}-12=0,\]由韦达定理得\[x_{1}+x_{4}=\dfrac{8k^{2}}{3+4k^{2}},x_{1}x_{4}=\dfrac{4k^{2}-12}{3+4k^{2}},\]所以\[\begin{split}|y_{1}-y_{4}|^{2}&=k^{2}|x_{1}-x_{4}|^{2}\\&=k^{2}\left[(x_{1}+x_{4})^{2}-4x_{1}x_{4}\right]\\&=\dfrac{k^{2}}{(3+4k^{2})^{2}}\left[64k^{4}-16(3+4k^{2})(k^{2}-3)\right]\\&=9\cdot \dfrac{16k^{2}(k^{2}+1)}{(3+4k^{2})^{2}}.\end{split}\]故平行四边形 $ABCD$ 的面积为\[S_{\text{平行四边形}ABCD}=2|y_{1}-y_{4}|=6\sqrt{\dfrac{16k^{2}(1+k^{2})}{(3+4k^{2})^{2}}}<6.\]当 $AD$ 的斜率不存在，即 $AD$ 垂直于 $x$ 轴时，易得 $A\left(1,\dfrac{3}{2}\right)$，$D\left(1,-\dfrac{3}{2}\right)$，则$$|AD|=3 , d=|F_{1}F_{2}|=2,$$故\[S_{\text{平行四边形}ABCD}=|AD|\cdot d=6.\]综上所述，平行四边形 $ABCD$ 的面积最大值为 $6$．
答案
解析
备注
