如图，$C$ 为半圆弧 $O$ 的中点，点 $P$ 为直径 $BA$ 延长线上一点，过点 $P$ 作半圆的切线 $PD$，$D$ 为切点，$\angle DPB$ 的平分线分别交 $AC$，$BC$ 与点 $E$，$F$．证明：$\angle PDA=\angle CDF$．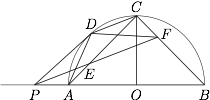
【难度】
【出处】
2014年全国高中数学联赛江西省预赛
【标注】
【答案】
略
【解析】
连结 $OD$，$DE$，如图．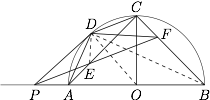
因为 $OD \perp PD$，$CO\perp PO$，所以$$\angle DPB +\angle DOP=\angle DOP +\angle DOC,$$故$$\angle DPB =\angle DOC=2\angle DAC =2\angle DBC=2\angle DPF,$$即$$\angle DAC =\angle DPE , \angle DPF =\angle DBF,$$所以 $P$，$A$，$E$，$D$ 与 $P$，$B$，$F$，$D$ 分别四点共圆，故$$\angle DEC =\angle DPA , \angle DFC =\angle DPA,$$即$$\angle DEC =\angle DFC ,$$所以 $D$，$E$，$F$，$C$ 四点共圆．因此$$\angle CDF =\angle CEF=\angle PEA =\angle PDA.$$
因为 $OD \perp PD$，$CO\perp PO$，所以$$\angle DPB +\angle DOP=\angle DOP +\angle DOC,$$故$$\angle DPB =\angle DOC=2\angle DAC =2\angle DBC=2\angle DPF,$$即$$\angle DAC =\angle DPE , \angle DPF =\angle DBF,$$所以 $P$，$A$，$E$，$D$ 与 $P$，$B$，$F$，$D$ 分别四点共圆，故$$\angle DEC =\angle DPA , \angle DFC =\angle DPA,$$即$$\angle DEC =\angle DFC ,$$所以 $D$，$E$，$F$，$C$ 四点共圆．因此$$\angle CDF =\angle CEF=\angle PEA =\angle PDA.$$
答案
解析
备注
