如图,在 $\triangle ABC$ 中,$\angle B=90^{\circ}$,它的内切圆分别与边 $BC,CA,AB$ 相切于点 $D,E,F$,连结 $AD$,与内切圆相交于另一点 $P$,连结 $PC$,$PE$,$PF$,$FD$,$ED$.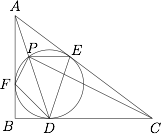

【难度】
【出处】
2013年全国高中数学联赛福建省预赛
【标注】
-
求证:$\dfrac{FP}{FD}=\dfrac{EP}{ED}$;标注答案略解析由条件知$$\angle AFP=\angle ADF,$$又因为$$\angle FAP=\angle FAD,$$所以$$\triangle AFP\backsim \triangle ADF,$$故$$\dfrac{AP}{AF}=\dfrac{FP}{DF}.$$同理,因为$$\angle AEP=\angle ADE , \angle PAE=\angle EAD,$$所以$$\triangle AEP\backsim \triangle ADE,$$故$$\dfrac{EP}{DE}=\dfrac{AP}{AE}.$$因为 $AF=AE$,所以$$\dfrac{EP}{DE}=\dfrac{AP}{AE}=\dfrac{AP}{AF}=\dfrac{FP}{DF},$$从而 $\dfrac{FP}{FD}=\dfrac{EP}{ED}$ 得证.
-
若 $PE\parallel BC$,求证:$PC\perp PF$.标注答案略解析因为 $PE\parallel BC$,所以\[\angle PED=\angle EDC=\angle DPE=\angle CED.\]所以$$\triangle DPE\backsim \triangle CDE.$$所以 $\dfrac{EP}{ED}=\dfrac{PD}{DC}$.结合第 $(1)$ 小问可知,$\dfrac{FP}{FD}=\dfrac{DP}{DC}$.又 $\angle PFD=\angle PDC$,所以$$\triangle PFD\backsim \triangle PDC,$$故 $\angle PCB=\angle PDF=\angle PFA$.所以 $P,F,B,C$ 四点共圆.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2