如图，圆 $O_1$ 与圆 $O_2$ 相交于 $P$，$Q$ 两点，且圆 $O_2$ 经过圆心 $O_1$．$A$ 是圆 $O_1$ 的优弧 $\widehat {PQ}$ 上一点，$AP$，$AQ$ 的延长线与圆 $ O_2$ 分别交于点 $B$，$C$．求证：$O_1$ 为 $\triangle ABC$ 的垂心．
【难度】
【出处】
2014年全国高中数学联赛陕西省预赛（二试）
【标注】
【答案】
略
【解析】
如图，连结 $PQ$，$O_1O_2$，$O_1P$，$O_1Q$，$O_1B$，则$$PQ \perp O_1O_2.$$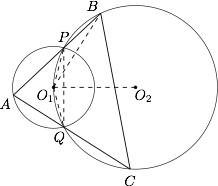
因为$$\angle BAC=\dfrac 12 \angle PO_1Q=\angle PO_1O_2 , \angle ABO_1= \angle PQO_1=\angle QPO_1 ,$$所以$$\angle BAC+ \angle ABO_1=\angle PO_1Q+\angle QPO_1=90^{\circ},$$故$$BO_1 \perp AC.$$同理可得，$$CO_1 \perp AB.$$故 $O_1$ 为 $\triangle ABC$ 的垂心．
因为$$\angle BAC=\dfrac 12 \angle PO_1Q=\angle PO_1O_2 , \angle ABO_1= \angle PQO_1=\angle QPO_1 ,$$所以$$\angle BAC+ \angle ABO_1=\angle PO_1Q+\angle QPO_1=90^{\circ},$$故$$BO_1 \perp AC.$$同理可得，$$CO_1 \perp AB.$$故 $O_1$ 为 $\triangle ABC$ 的垂心．
答案
解析
备注
