如图，设 $D$ 是锐角 $\triangle ABC$ 内部的一个点，使得 $\angle ADB=\angle ACB+90^{\circ}$，并且 $AC \cdot BD=AD \cdot BC$，计算比值 $\dfrac {AB\cdot AD}{AC \cdot BD}$．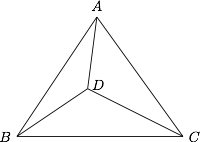
【难度】
【出处】
2014年全国高中数学联赛黑龙江省预赛
【标注】
【答案】
$\sqrt 2$
【解析】
如图，从 $D$ 向 $\triangle ABC$ 三边引垂线，垂足分别为 $E$，$F$，$G$，连结 $EF$，$FG$，$GE$．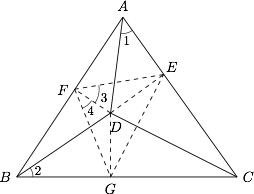
因为 $A$，$F$，$D$，$E$ 四点共圆，$AD$ 为直径，由正弦定理得$$\dfrac {EF}{AD}=\sin \angle A=\dfrac {BC}{2R}$$（$R$ 为 $\triangle ABC$ 的外接圆半径），
故$$EF=\dfrac {1}{2R}AD \cdot BC.$$同理$$FG=\dfrac {1}{2R}AC \cdot BD, GE=\dfrac {1}{2R}AB \cdot CD.$$因为$$AC \cdot BD=AD \cdot BC,$$所以 $EF=FG$．
由$$\angle ADB=\angle ACB+90^{\circ},$$得 $\angle 1+\angle 2=90^{\circ}$，而$$\angle 3=\angle 1 , \angle 4=\angle 2,$$因此 $\angle EFG=90^{\circ}$，$\triangle EFG$ 为等腰直角三角形，故$$\dfrac {AB\cdot CD}{AC \cdot BD}=\dfrac {GE}{FG}=\sqrt 2.$$
因为 $A$，$F$，$D$，$E$ 四点共圆，$AD$ 为直径，由正弦定理得$$\dfrac {EF}{AD}=\sin \angle A=\dfrac {BC}{2R}$$（$R$ 为 $\triangle ABC$ 的外接圆半径），故$$EF=\dfrac {1}{2R}AD \cdot BC.$$同理$$FG=\dfrac {1}{2R}AC \cdot BD, GE=\dfrac {1}{2R}AB \cdot CD.$$因为$$AC \cdot BD=AD \cdot BC,$$所以 $EF=FG$．
由$$\angle ADB=\angle ACB+90^{\circ},$$得 $\angle 1+\angle 2=90^{\circ}$，而$$\angle 3=\angle 1 , \angle 4=\angle 2,$$因此 $\angle EFG=90^{\circ}$，$\triangle EFG$ 为等腰直角三角形，故$$\dfrac {AB\cdot CD}{AC \cdot BD}=\dfrac {GE}{FG}=\sqrt 2.$$
答案
解析
备注
