设平面点集 $A=\left\{(x,y) \bigg| (y-x)\cdot\left(y-\dfrac{18}{25x}\right)\geqslant0\right\}$，$B=\{(x,y)\mid(x-1)^2+(y-1)^2\leqslant1\}$．若 $(x,y)\in A\cap B$，求 $2x-y$ 的最小值．
【难度】
【出处】
2015年全国高中数学联赛湖北省预赛
【标注】
【答案】
$-1$
【解析】
作出平面点集 $A,B$ 所表示的平面区域，$A\cap B$ 表示如图阴影部分 $D$．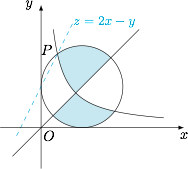
令 $z=2x-y$，则 $y=2x-z$，$-z$ 表示直线的纵截距，容易知道直线经过区域 $D$ 中的点 $P$ 时，$z$ 最小．
因为点 $P$ 在圆 $(x-1)^2+(y-1)^2=1$ 上，设它的坐标为 $(1+\cos\theta,1+\sin\theta)$，结合图形可知 $\theta\in\left(\dfrac{\pi}{2},\pi\right)$．
又点 $P$ 在曲线 $y=\dfrac{18}{25x}$ 上，所以有$$(1+\cos\theta)(1+\sin\theta)=\dfrac{18}{25},$$即$$\sin\theta\cos\theta+\sin\theta+\cos\theta+\dfrac{7}{25}.$$设 $\sin\theta+\cos\theta=t$，则$$\sin\theta\cos\theta=\dfrac12(t^2-1),$$代入得$$\dfrac12(t^2-1)+t+\dfrac{7}{25}=0,$$解得 $t=\dfrac15$ 或 $t=-\dfrac{11}{5}$（舍），即$$\sin\theta+\cos\theta=\dfrac15.$$结合 $\sin^2\theta+\cos^2\theta=1$，并注意到 $\theta\in\left(\dfrac{\pi}{2},\pi\right)$，解得$$\sin\theta=\dfrac45,\cos\theta=-\dfrac35.$$所以点 $P$ 的坐标为 $\left(\dfrac25,\dfrac95\right)$．
因此，$z$ 的最小值为 $-1$．
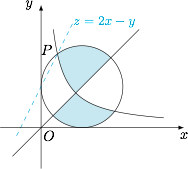令 $z=2x-y$，则 $y=2x-z$，$-z$ 表示直线的纵截距，容易知道直线经过区域 $D$ 中的点 $P$ 时，$z$ 最小．因为点 $P$ 在圆 $(x-1)^2+(y-1)^2=1$ 上，设它的坐标为 $(1+\cos\theta,1+\sin\theta)$，结合图形可知 $\theta\in\left(\dfrac{\pi}{2},\pi\right)$．
又点 $P$ 在曲线 $y=\dfrac{18}{25x}$ 上，所以有$$(1+\cos\theta)(1+\sin\theta)=\dfrac{18}{25},$$即$$\sin\theta\cos\theta+\sin\theta+\cos\theta+\dfrac{7}{25}.$$设 $\sin\theta+\cos\theta=t$，则$$\sin\theta\cos\theta=\dfrac12(t^2-1),$$代入得$$\dfrac12(t^2-1)+t+\dfrac{7}{25}=0,$$解得 $t=\dfrac15$ 或 $t=-\dfrac{11}{5}$（舍），即$$\sin\theta+\cos\theta=\dfrac15.$$结合 $\sin^2\theta+\cos^2\theta=1$，并注意到 $\theta\in\left(\dfrac{\pi}{2},\pi\right)$，解得$$\sin\theta=\dfrac45,\cos\theta=-\dfrac35.$$所以点 $P$ 的坐标为 $\left(\dfrac25,\dfrac95\right)$．
因此，$z$ 的最小值为 $-1$．
答案
解析
备注
