已知平面凸四边形 $ABCD$ 的面积为 $1$，求证：$$|AB|+|AC|+|AD|+|BC|+|BD|+|CD|\geqslant 4+2\sqrt 2.$$
【难度】
【出处】
2014年全国高中数学联赛安徽省预赛
【标注】
【答案】
略
【解析】
假设凸四边形 $ABCD$ 满足 $L=|AB|+|AC|+|AD|+|BC|+|BD|+|CD|$ 最小．此时 $ABCD$ 一定是菱形，否则，如图所示，可固定两对角点（不妨设是 $B$，$D$），过 $A$，$C$ 分别作 $BD$ 的平行线，调整另外两点 $A$，$C$ 的位置，使它们分别位于两平行线上，则 $\triangle ABD$ 和 $\triangle CBD$ 的面积都不变，但 $L$ 变大．从而$$AB=AD , BC=CD.$$类似地，$$AB=BC , CD=DA,$$即 $ABCD$ 是菱形．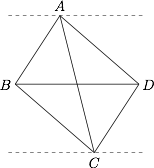
设菱形 $ABCD$ 的两条对角线长度分别是 $x$，$y$，则$$xy=2 , L=x+y+2\sqrt {x^2+y^2}.$$根据均值不等式$$L=x+y+2\sqrt {x^2+y^2}\geqslant 2\sqrt {xy}+2\sqrt {2xy}=4+2\sqrt 2,$$当 $x=y=\sqrt 2$ 时，$L$ 取得最小值 $4+2\sqrt 2$．
设菱形 $ABCD$ 的两条对角线长度分别是 $x$，$y$，则$$xy=2 , L=x+y+2\sqrt {x^2+y^2}.$$根据均值不等式$$L=x+y+2\sqrt {x^2+y^2}\geqslant 2\sqrt {xy}+2\sqrt {2xy}=4+2\sqrt 2,$$当 $x=y=\sqrt 2$ 时，$L$ 取得最小值 $4+2\sqrt 2$．
答案
解析
备注
