如图:四棱锥 $P-ABCD$,$PA \perp \text{平面}ABCD$,且 $PA=4$,底面 $ABCD$ 为直角梯形,$\angle CDA=\angle BAD=90^{\circ}$,$AB=2$,$CD=1$,$AD=\sqrt 2$,$M$,$N$ 分别为 $PD$,$PB$ 的中点,平面 $MCN$ 与 $PA$ 交点为 $Q$.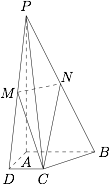

【难度】
【出处】
2010年全国高中数学联赛河北省预赛
【标注】
-
求 $PQ$ 的长度;标注答案$PQ=1$解析取 $AP$ 的中点 $E$,连结 $ED$,则 $ED \parallel CN$,再取 $EP$ 的中点即为所求点 $Q$.
因为 $MQ \parallel ED$,故$$MQ \parallel CN,$$所以 $M$,$N$,$C$,$Q$ 四点共面.
因此平面 $MCN$ 与 $AP$ 的交点 $Q$ 即为 $AP$ 的四等分点,所以 $PQ=1$. -
求截面 $MCN$ 与底面 $ABCD$ 所成二面角的大小;标注答案$\dfrac {\pi}{3}$解析易证$$\text{平面}MEN \parallel \text{底面}ABCD,$$所以截面 $MCN$ 与平面 $MEN$ 所成的二面角即为截面 $MCN$ 与底面 $ABCD$ 所成的二面角.
因为 $PA \perp \text{底面}ABCD$,所以$$PA \perp \text{平面}MEN.$$过 $E$ 作 $EF \perp MN$,垂足为 $F$,连结 $QF$,由三垂线定理可得$$QF \perp MN,$$所以 $\angle QFE$ 为截面 $MCN$ 与平面 $MEN$ 所成二面角的平面角.
在直角三角形 $MEN$ 中,$$ME=\dfrac {\sqrt 2}{2} , EN=1 , MN=\dfrac {\sqrt 6}{2},$$则 $EF=\dfrac {\sqrt 3}{3}$,所以$$\tan \angle QFE=\sqrt 3,$$故 $\angle QFE=\dfrac {\pi}{3}$. -
求点 $A$ 到平面 $MCN$ 的距离.标注答案$1$解析因为 $EP$ 的中点为点 $Q$,且平面 $MCN$ 与 $PA$ 交于点 $Q$,所以点 $A$ 到平面 $MCN$ 的距离即为点 $E$ 到平面 $MCN$ 的距离的 $2$ 倍.
由 $(2)$ 知$$MN\perp \text{平面}QEF, \text{平面}MCNQ \perp \text{平面}QEF$$且 $\text{平面}MCNQ$ 与 $\text{平面}QEF$ 的交线为 $QF$.过 $E$ 作 $EH\perp QF$,垂足为 $H$,则 $EH \perp \text{平面}QEF $,$EH$ 为点 $E$ 到平面 $MCN$ 的距离.
在直角三角形 $EQF$ 中,$$EF=\dfrac {\sqrt 3}{3} , \angle QFE=\dfrac {\pi}{3},$$故 $EH=\dfrac 12$.
因此点 $A$ 到平面 $MCN$ 的距离为 $1$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3