如图,平面 $m\parallel$ 平面 $n$,线段 $AD$ 分别交 $m$ 和 $n$ 于点 $B$ 和 $C$,过点 $A$ 的另一直线分别交 $m$ 和 $n$ 于点 $M$ 和点 $P$,过点 $D$ 的另一直线分别交 $m$ 和 $n$ 于点 $N$ 和点 $Q$.已知 $\dfrac{S_{\triangle{BMN}}}{S_{\triangle{CPQ}}}=\dfrac 32$,求 $\dfrac{AD}{CD}$ 的最小值.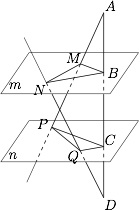

【难度】
【出处】
2009年全国高中数学联赛山东省预赛
【标注】
【答案】
$3+\sqrt 3$
【解析】
由平面 $m\parallel$ 平面 $n$,知$$BM\parallel CP , BN\parallel CQ,$$所以有$$\sin{\angle{MBN}}=\sin{\angle{PCQ}},$$且$$\dfrac{BM}{CP}=\dfrac{AB}{AC},\dfrac{BN}{CQ}=\dfrac{BD}{CD}.$$又因为\[\begin{split}S_{\triangle{BMN}}&=\dfrac 12 BM\cdot BN\cdot \sin{\angle{MBN}},\\ S_{\triangle{CPQ}}&=\dfrac 12 CP\cdot CQ \cdot \sin{\angle{PCQ}},\end{split}\]由 $\dfrac{S_{\triangle{BMN}}}{S_{\triangle{CPQ}}}=\dfrac 32$,得$$\dfrac{AB}{AC}\cdot \dfrac{BD}{CD}=\dfrac 32.$$令 $\dfrac{AC}{AB}=\alpha$,$\dfrac{BD}{CD}=\beta$,则 $2\beta =3\alpha$,且 $\beta>\alpha >1$.
又因为$$\dfrac{BC}{AB}=\dfrac{AC-AB}{AB}=\alpha -1 , \dfrac{BC}{CD}=\dfrac {BD-CD}{CD}=\beta-1,$$所以$$AB=\dfrac {\beta-1}{\alpha -1}CD,BC=(\beta-1)CD,$$故\[\begin{split}\dfrac{AD}{CD}&=\dfrac{AB+BC+CD}{CD}\\&=\dfrac {\beta-1}{\alpha-1}+\beta\\&=\dfrac{3\alpha ^2 -2}{2(\alpha -1)}\\&=\dfrac 32\left[(\alpha -1)+\dfrac 1{3(\alpha -1)}\right]+3\\&\geqslant 3+\sqrt 3,\end{split}\]显然,当 $\alpha -1=\dfrac{\sqrt 3}{3}$,即 $\alpha =1+\dfrac{\sqrt 3}{3}$ 时,有$$\dfrac{AD}{CD}=3+\sqrt 3,$$所以 $\dfrac{AD}{CD}$ 的最小值为 $3+\sqrt 3$.
又因为$$\dfrac{BC}{AB}=\dfrac{AC-AB}{AB}=\alpha -1 , \dfrac{BC}{CD}=\dfrac {BD-CD}{CD}=\beta-1,$$所以$$AB=\dfrac {\beta-1}{\alpha -1}CD,BC=(\beta-1)CD,$$故\[\begin{split}\dfrac{AD}{CD}&=\dfrac{AB+BC+CD}{CD}\\&=\dfrac {\beta-1}{\alpha-1}+\beta\\&=\dfrac{3\alpha ^2 -2}{2(\alpha -1)}\\&=\dfrac 32\left[(\alpha -1)+\dfrac 1{3(\alpha -1)}\right]+3\\&\geqslant 3+\sqrt 3,\end{split}\]显然,当 $\alpha -1=\dfrac{\sqrt 3}{3}$,即 $\alpha =1+\dfrac{\sqrt 3}{3}$ 时,有$$\dfrac{AD}{CD}=3+\sqrt 3,$$所以 $\dfrac{AD}{CD}$ 的最小值为 $3+\sqrt 3$.
答案
解析
备注