如图，点 $H$ 为 $\triangle ABC$ 的垂心，以 $AB$ 为直径的 $\odot O_{1}$ 和 $\triangle BCH$ 的外接圆 $\odot O_{2}$ 相交于点 $D$，延长 $AD$ 交 $CH$ 于点 $P$，求证：点 $P$ 为 $CH$ 的中点．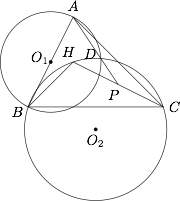
【难度】
【出处】
2016年全国高中数学联赛广西壮族自治区预赛
【标注】
【答案】
略
【解析】
如图，延长 $AP$ 交 $\odot O_{2}$ 于点 $Q$，连结 $AH,BD,QB,QC,QH$．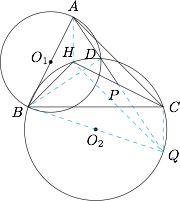
因为 $AB$ 为 $\odot O_{1}$ 的直径，所以$$\angle BDQ=180^\circ-\angle ADB==90^{\circ},$$故 $BD$ 为 $\odot O_{2}$ 的直径，
所以$$CQ\perp BC , BH\perp HQ.$$又点 $H$ 为 $\triangle ABC$ 的垂心，所以$$AH\perp BC , BH\perp AC,$$于是$$AH\parallel CQ , AC\parallel HQ,$$四边形 $ACQH$ 为平行四边形，因此点 $P$ 为 $CH$ 的中点．
因为 $AB$ 为 $\odot O_{1}$ 的直径，所以$$\angle BDQ=180^\circ-\angle ADB==90^{\circ},$$故 $BD$ 为 $\odot O_{2}$ 的直径，所以$$CQ\perp BC , BH\perp HQ.$$又点 $H$ 为 $\triangle ABC$ 的垂心，所以$$AH\perp BC , BH\perp AC,$$于是$$AH\parallel CQ , AC\parallel HQ,$$四边形 $ACQH$ 为平行四边形，因此点 $P$ 为 $CH$ 的中点．
答案
解析
备注
