已知四边形 $PQRS$ 是圆内接四边形,$\angle PSR=90^\circ$,过点 $Q$ 作 $PR,PS$ 的垂线,垂足分别为点 $H,K$.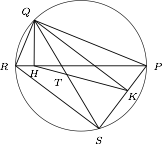

【难度】
【出处】
2012年全国高中数学联赛黑龙江省预赛
【标注】
-
求证:$Q,H,K,P$ 四点共圆;标注答案略解析因为$$\angle PHQ=\angle PKQ=90^\circ,$$所以 $Q,H,K,P$ 四点共圆.
-
求证:$QT=TS$.标注答案略解析因为 $Q,H,K,P$ 四点共圆,所以$$\angle HKS=\angle HQP.\qquad\qquad\cdots\cdots\text{ ① }$$因为 $\angle PSR=90^\circ$,所以 $PR$ 为圆的直径,所以 $\angle PQR=90^\circ$,故$$\angle QRH=\angle HQP.\qquad\qquad\cdots\cdots\text{ ② }$$又因为$$\angle QSP=\angle QRH,\qquad\qquad\cdots\cdots\text{ ③ }$$结合 $\text{ ①②③ }$ 得,$$\angle SQP=\angle HKS , TS=TK.$$又 $\angle SKQ=90^\circ$,因为 $\angle SQK=\angle TKQ$,所以 $QT=TK$,故 $QT=TS$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2