已知三棱锥的三条侧棱两两垂直，底面积为 $1$，求此三棱锥体积的最大值．
【难度】
【出处】
2012年全国高中数学联赛新疆省预赛
【标注】
【答案】
$\dfrac13\sqrt[4]{\dfrac{4}{27}}$
【解析】
如图，三棱锥 $P-ABC$ 中，$PA,PB,PC$ 两两垂直．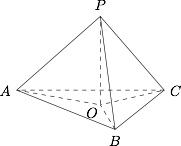
不妨设侧面 $APB$，侧面 $BPC$，侧面 $APC$，与底面 $ABC$ 所成的角分别为 $\alpha,\beta,\gamma$．
依题意$$S_{\triangle ABC}=1 , PC\perp\text{面}APB,$$所以 $\triangle ABC$ 在平面 $APB$ 内的射影为 $\triangle APB$．
由射影面积公式得$$\cos\alpha=\dfrac{S_{\triangle APB}}{S_{\triangle ABC}},$$即$$S_{\triangle APB}=S_{\triangle ABC}\cos\alpha=\cos\alpha.$$同理，$$\begin{split}S_{\triangle BPC}=\cos\beta,\\S_{\triangle APC}=\cos\gamma.\end{split}$$设点 $P$ 在底面 $ABC$ 内的射影为 $O$，连接 $AO,BO,CO$．
因为 $PA,PB,PC$ 两两垂直，易证 $\triangle ABC$ 必为锐角三角形，且 $O$ 是 $\triangle ABC$ 的垂心，故点 $O$ 必在 $\triangle ABC$ 的内部．
由射影面积公式，得$$\cos\alpha=\dfrac{S_{\triangle AOB}}{S_{\triangle APB}},$$故$$S_{\triangle AOB}=\cos^2\alpha.$$同理$$\begin{split}S_{\triangle BOC}=\cos^2\beta,\\S_{\triangle AOC}=\cos^2\gamma,\end{split}$$于是$$1=S_{\triangle ABC}=S_{\triangle AOB}+S_{\triangle BOC}+S_{\triangle AOC}=\cos^2\alpha+\cos^2\beta+\cos^2\gamma.$$接下来求其体积．
因为$$S_{\triangle APB}=\dfrac12\cdot PA\cdot PB=\cos\alpha,$$因此$$PA\cdot PB=2\cos\alpha.$$同理$$\begin{split}PB\cdot PC=2\cos\beta,\\PA\cdot PC=2\cos\gamma,\end{split}$$三式相乘可得$$PA\cdot PB\cdot PC=2\sqrt{2\cos\alpha\cos\beta\cos\gamma},$$则$$V=\dfrac16\cdot PA\cdot PB\cdot PC=\dfrac13\sqrt{2\cos\alpha\cos\beta\cos\gamma}.$$由均值不等式$$\dfrac{x+y+z}{3}\geqslant\sqrt[3]{xyz},$$得$$\dfrac{\cos^2\alpha+\cos^2\beta+\cos^2\gamma}{3}\geqslant\sqrt[3]{\cos^2\alpha\cos^2\beta\cos^2\gamma},$$即$$\cos^2\alpha\cos^2\beta\cos^2\gamma\leqslant\dfrac{1}{27},$$故$$\sqrt{\cos\alpha\cos\beta\cos\gamma}\leqslant\sqrt[4]{\dfrac{1}{27}},$$所以$$V\leqslant\dfrac13\sqrt[4]{\dfrac{4}{27}},$$当且仅当 $\cos\alpha=\cos\beta=\cos\gamma=\dfrac{\sqrt3}{3}$，即 $\alpha=\beta=\gamma=\arccos\dfrac{\sqrt3}{3}$ 时取等号．
不妨设侧面 $APB$，侧面 $BPC$，侧面 $APC$，与底面 $ABC$ 所成的角分别为 $\alpha,\beta,\gamma$．依题意$$S_{\triangle ABC}=1 , PC\perp\text{面}APB,$$所以 $\triangle ABC$ 在平面 $APB$ 内的射影为 $\triangle APB$．
由射影面积公式得$$\cos\alpha=\dfrac{S_{\triangle APB}}{S_{\triangle ABC}},$$即$$S_{\triangle APB}=S_{\triangle ABC}\cos\alpha=\cos\alpha.$$同理，$$\begin{split}S_{\triangle BPC}=\cos\beta,\\S_{\triangle APC}=\cos\gamma.\end{split}$$设点 $P$ 在底面 $ABC$ 内的射影为 $O$，连接 $AO,BO,CO$．
因为 $PA,PB,PC$ 两两垂直，易证 $\triangle ABC$ 必为锐角三角形，且 $O$ 是 $\triangle ABC$ 的垂心，故点 $O$ 必在 $\triangle ABC$ 的内部．
由射影面积公式，得$$\cos\alpha=\dfrac{S_{\triangle AOB}}{S_{\triangle APB}},$$故$$S_{\triangle AOB}=\cos^2\alpha.$$同理$$\begin{split}S_{\triangle BOC}=\cos^2\beta,\\S_{\triangle AOC}=\cos^2\gamma,\end{split}$$于是$$1=S_{\triangle ABC}=S_{\triangle AOB}+S_{\triangle BOC}+S_{\triangle AOC}=\cos^2\alpha+\cos^2\beta+\cos^2\gamma.$$接下来求其体积．
因为$$S_{\triangle APB}=\dfrac12\cdot PA\cdot PB=\cos\alpha,$$因此$$PA\cdot PB=2\cos\alpha.$$同理$$\begin{split}PB\cdot PC=2\cos\beta,\\PA\cdot PC=2\cos\gamma,\end{split}$$三式相乘可得$$PA\cdot PB\cdot PC=2\sqrt{2\cos\alpha\cos\beta\cos\gamma},$$则$$V=\dfrac16\cdot PA\cdot PB\cdot PC=\dfrac13\sqrt{2\cos\alpha\cos\beta\cos\gamma}.$$由均值不等式$$\dfrac{x+y+z}{3}\geqslant\sqrt[3]{xyz},$$得$$\dfrac{\cos^2\alpha+\cos^2\beta+\cos^2\gamma}{3}\geqslant\sqrt[3]{\cos^2\alpha\cos^2\beta\cos^2\gamma},$$即$$\cos^2\alpha\cos^2\beta\cos^2\gamma\leqslant\dfrac{1}{27},$$故$$\sqrt{\cos\alpha\cos\beta\cos\gamma}\leqslant\sqrt[4]{\dfrac{1}{27}},$$所以$$V\leqslant\dfrac13\sqrt[4]{\dfrac{4}{27}},$$当且仅当 $\cos\alpha=\cos\beta=\cos\gamma=\dfrac{\sqrt3}{3}$，即 $\alpha=\beta=\gamma=\arccos\dfrac{\sqrt3}{3}$ 时取等号．
答案
解析
备注
