如图，在锐角 $\triangle ABC$ 中，$AB>AC$，$M,N$ 是 $BC$ 边上不同的两点，使得 $\angle BAM=\angle CAN$．设 $\triangle ABC$ 和 $\triangle AMN$ 的外心分别为 $O_1,O_2$，求证：$O_1,O_2,A$ 三点共线．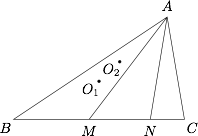
【难度】
【出处】
2012年全国高中数学联赛（二试）
【标注】
【答案】
略
【解析】
如图．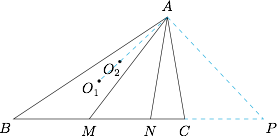
连接 $AO_1,AO_2$，过 $A$ 作 $AO_1$ 的垂线 $AP$ 交 $BC$ 的延长线于点 $P$，则 $AP$ 是圆 $O_1$ 的切线，所以$$\angle B=\angle PAC.$$又因为 $\angle BAM=\angle CAN$，所以$$\angle AMP=\angle B+\angle BAM=\angle PAC+\angle CAN=\angle PAN,$$因而 $AP$ 是 $\triangle AMN$ 外接圆 $O_2$ 的切线，故 $AP\perp AO_2$．
因为$$AP\perp AO_1 , AP\perp AO_2,$$所以 $O_1,O_2,A$ 三点共线．
连接 $AO_1,AO_2$，过 $A$ 作 $AO_1$ 的垂线 $AP$ 交 $BC$ 的延长线于点 $P$，则 $AP$ 是圆 $O_1$ 的切线，所以$$\angle B=\angle PAC.$$又因为 $\angle BAM=\angle CAN$，所以$$\angle AMP=\angle B+\angle BAM=\angle PAC+\angle CAN=\angle PAN,$$因而 $AP$ 是 $\triangle AMN$ 外接圆 $O_2$ 的切线，故 $AP\perp AO_2$．因为$$AP\perp AO_1 , AP\perp AO_2,$$所以 $O_1,O_2,A$ 三点共线．
答案
解析
备注
