如图，设 $H$ 为锐角 $\triangle ABC$ 的垂心，过点 $H$ 且垂直于 $BH$ 的直线交 $AB$ 于点 $D$，过点 $H$ 且垂直于 $CH$ 的直线交 $AC$ 于点 $E$，过点 $C$ 且垂直于 $BC$ 的直线交直线 $DE$ 于点 $F$．求证：$FH=FC$．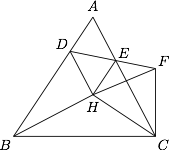
【难度】
【出处】
2015年全国高中数学联赛陕西省预赛（二试）
【标注】
【答案】
略
【解析】
如图，延长 $CF,HE$ 交于点 $G$，连接 $AH$ 交 $DE$ 于点 $M$．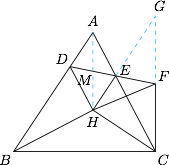
因为$$DH\perp BH , AC\perp BH,$$所以 $DH\parallel AC$．
同理 $EH\parallel AB$，故四边形 $ADHE$ 为平行四边形，所以 $M$ 为 $AH$ 的中点．
因为$$GC\perp BC , AH\perp BC,$$所以 $GC\parallel AH$，故 $\triangle CEG\backsim\triangle AEH$．
又 $M$ 为 $AH$ 的中点，所以 $F$ 为 $CG$ 的中点．
因此，在 $\mathrm{Rt}\triangle GHC$ 中，有$$FH=\dfrac12GC=FC.$$
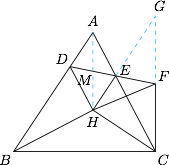因为$$DH\perp BH , AC\perp BH,$$所以 $DH\parallel AC$．同理 $EH\parallel AB$，故四边形 $ADHE$ 为平行四边形，所以 $M$ 为 $AH$ 的中点．
因为$$GC\perp BC , AH\perp BC,$$所以 $GC\parallel AH$，故 $\triangle CEG\backsim\triangle AEH$．
又 $M$ 为 $AH$ 的中点，所以 $F$ 为 $CG$ 的中点．
因此，在 $\mathrm{Rt}\triangle GHC$ 中，有$$FH=\dfrac12GC=FC.$$
答案
解析
备注
