如图,$\odot O_1$ 与 $\odot O_2$ 内切于点 $P$,$\odot O_1$ 的弦 $AB$ 切 $\odot O_2$ 于点 $C$,延长 $PC$ 交 $\odot O_1$ 于点 $G$,$PA$,$PB$ 分别交 $\odot O_2$ 于点 $E$,$F$,$EF$ 交 $PC$ 于点 $D$,延长 $AD$ 交 $\odot O_1$ 于点 $H$.求证: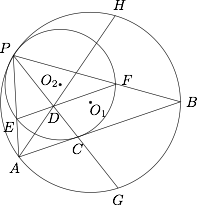

【难度】
【出处】
2010年全国高中数学联赛辽宁省预赛
【标注】
-
$G$ 为弧 $AB$ 的中点;标注答案略解析过 $P$ 作 $\odot O_1$ 的切线,在此切线上 $P$ 点左侧取一点 $Q$,则$$\angle QPC=\angle ACP,$$于是$$\angle QPA+\angle APG=\angle GPB+\angle PBC,$$而$$\angle QPA=\angle PBC,$$所以$$\angle APG=\angle GPB,$$于是 $G$ 为弧 $AB$ 的中点.
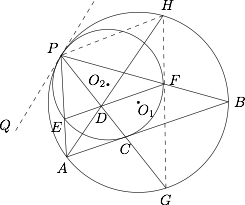
-
$G$,$F$,$H$ 三点共线.标注答案略解析连结 $PH$,可知$$\angle QPA=\angle PFD , \angle QPA=\angle PHD,$$所以 $ \angle PFD=\angle PHD$,因此 $P$,$D$,$F$,$H$ 四点共圆,所以$$\angle DHF=\angle DPF=\angle GPB , \angle DHG=\angle APG.$$又因为 $\angle APG=\angle GPB $,所以$$\angle DHF=\angle DHG,$$于是 $G$,$F$,$H$ 三点共线.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2