给定 $y$ 轴上的一点 $A(0,a)$($a>1$),对于曲线 $y=\left
|\dfrac 12 x^2-1\right|$ 上的动点 $M(x,y)$,试求 $A,M$ 两点之间距离 $|AM|$ 的最小值(用 $a$ 表示).
|\dfrac 12 x^2-1\right|$ 上的动点 $M(x,y)$,试求 $A,M$ 两点之间距离 $|AM|$ 的最小值(用 $a$ 表示).
【难度】
【出处】
2009年全国高中数学联赛江西省预赛
【标注】
【答案】
$|AM|_{\min}=\begin{cases}a-1,& 1<a\leqslant 4,\\ \sqrt{2a+1},&a>4.\end{cases}$
【解析】
如图,易求得曲线上诸点的坐标为:$E(-\sqrt 2,0),F(\sqrt 2,0),D(0,1)$.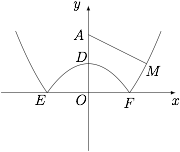
情形一 当 $x^2<2$,即 $-\sqrt 2\leqslant x \leqslant \sqrt 2$ 时,曲线方程为$$y=1-\dfrac{x^2}{2},$$显然当 $M$ 位于顶点 $D$ 处时,距离 $|AM|$ 取得最小值$$|AM|=|AD|=a-1.$$情形二 当 $x^2<2$ 时,曲线方程为$$y=\dfrac{x^2}{2}-1.$$设点 $M\left(x,\dfrac{x^2}{2}-1\right)$,由于\[\begin{split}|AM|^2&=x^2+\left(\dfrac{x^2}{2}-1-a\right)^2\\&=\dfrac 14(x^2-2a)^2+2a+1,\end{split}\]而 $a>1$,所以$$2a>2 , \sqrt{2a}>\sqrt 2,$$于是当 $x=\sqrt{2a}$ 时,$|AM|$ 取得最小值 $\sqrt{2a+1}$.
再比较两种情形下的 $|AM|$ 最小值的大小:
令\[\begin{split}f(a)&=(a-1)^2-(2a+1)\\&=a(a-4),\end{split}\]则当 $1<a\leqslant 4$ 时,$f(a)\leqslant 0$,$|AM|$ 的最小值为$$|AM|=a-1.$$当 $a>4$ 时,$f(a)>0$,则最小值$$|AM|=\sqrt{2a+1}.$$因此$$|AM|_{\min}=\begin{cases}a-1,& 1<a\leqslant 4,\\ \sqrt{2a+1},&a>4.\end{cases}$$

再比较两种情形下的 $|AM|$ 最小值的大小:
令\[\begin{split}f(a)&=(a-1)^2-(2a+1)\\&=a(a-4),\end{split}\]则当 $1<a\leqslant 4$ 时,$f(a)\leqslant 0$,$|AM|$ 的最小值为$$|AM|=a-1.$$当 $a>4$ 时,$f(a)>0$,则最小值$$|AM|=\sqrt{2a+1}.$$因此$$|AM|_{\min}=\begin{cases}a-1,& 1<a\leqslant 4,\\ \sqrt{2a+1},&a>4.\end{cases}$$
答案
解析
备注