如图，$AB,CD,EF$ 是一个圆中三条不相交的弦，以其中每两条弦为一组对边，各得到一个凸四边形，设这三个四边形的对角线的交点分别为 $M,N,P$．证明：$M,N,P$ 三点共线．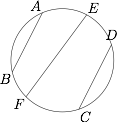
【难度】
【出处】
2009年全国高中数学联赛江西省预赛
【标注】
【答案】
略
【解析】
如图，设 $AB,CD,EF$ 为三条不相交的弦，其中$$AC\cap BD=P , AF\cap BE=M , CE\cap DF=N.$$
又设 $BD\cap CE=H$，点 $N,P,M$ 截 $\triangle{BEH}$ 的三边．
根据梅涅劳斯定理，要证明 $N,P,M$ 三点共线只要证$$\dfrac{HP}{PB}\cdot \dfrac{BM}{ME}\cdot \dfrac{EN}{NH}=1.\cdots {\text{ ① }}$$用记号 $\overline{\Delta}$ 表示三角形面积，则\[\begin{split}&{\begin{split}\dfrac{BM}{ME}=\dfrac{\overline{\Delta}BAF}{\overline{\Delta}EAF}=\dfrac{BA\cdot BF}{EA\cdot EF},\cdots \text{ ② }\end{split}}\\&{\begin{split}\dfrac{HP}{PB}&=\dfrac{\overline{\Delta}HAC}{\overline{\Delta}BAC}\\&=\dfrac{\overline{\Delta}HAC}{\overline{\Delta}EAC}\cdot \dfrac{\overline{\Delta}EAC}{\overline{\Delta}BAC}\\&=\dfrac{CH}{CE}\cdot \dfrac{EA\cdot EC}{BA\cdot BC}\\&=\dfrac{CH\cdot EA}{BA\cdot BC},\cdots \text{ ③ }\end{split}}\end{split}\]由此得$$\dfrac{HP}{PB}\cdot \dfrac{BM}{ME}=\dfrac{CH\cdot BF}{BC\cdot EF},$$因此只要证$$\dfrac{EN\cdot BF}{EF\cdot BC}\cdot \dfrac{CH}{NH}=1.\cdots {\text{ ④ }}$$注意 $\dfrac{EN}{EF}=\dfrac{DN}{DC}$，$\angle{BFD}=\angle{BCD}$，则\[\begin{split}\dfrac{NH}{CH}&=\dfrac{\overline{\Delta}NBD}{\overline{\Delta}CBD}\\&=\dfrac{\overline{\Delta}FBD-\overline{\Delta}FBN}{\overline{\Delta}CBD}\\&=\dfrac{FB\cdot FD-FB\cdot FN}{CB\cdot CD}\\&=\dfrac{FB\cdot ND}{CB\cdot CD}\\&=\dfrac{FB}{CB}\cdot \dfrac{EN}{EF},\end{split}\]所以$$\dfrac{EN\cdot BF}{EF\cdot BC}\cdot \dfrac{CH}{NH}=1,$$即 ④ 成立，从而 ① 成立，故结论得证
又设 $BD\cap CE=H$，点 $N,P,M$ 截 $\triangle{BEH}$ 的三边．根据梅涅劳斯定理，要证明 $N,P,M$ 三点共线只要证$$\dfrac{HP}{PB}\cdot \dfrac{BM}{ME}\cdot \dfrac{EN}{NH}=1.\cdots {\text{ ① }}$$用记号 $\overline{\Delta}$ 表示三角形面积，则\[\begin{split}&{\begin{split}\dfrac{BM}{ME}=\dfrac{\overline{\Delta}BAF}{\overline{\Delta}EAF}=\dfrac{BA\cdot BF}{EA\cdot EF},\cdots \text{ ② }\end{split}}\\&{\begin{split}\dfrac{HP}{PB}&=\dfrac{\overline{\Delta}HAC}{\overline{\Delta}BAC}\\&=\dfrac{\overline{\Delta}HAC}{\overline{\Delta}EAC}\cdot \dfrac{\overline{\Delta}EAC}{\overline{\Delta}BAC}\\&=\dfrac{CH}{CE}\cdot \dfrac{EA\cdot EC}{BA\cdot BC}\\&=\dfrac{CH\cdot EA}{BA\cdot BC},\cdots \text{ ③ }\end{split}}\end{split}\]由此得$$\dfrac{HP}{PB}\cdot \dfrac{BM}{ME}=\dfrac{CH\cdot BF}{BC\cdot EF},$$因此只要证$$\dfrac{EN\cdot BF}{EF\cdot BC}\cdot \dfrac{CH}{NH}=1.\cdots {\text{ ④ }}$$注意 $\dfrac{EN}{EF}=\dfrac{DN}{DC}$，$\angle{BFD}=\angle{BCD}$，则\[\begin{split}\dfrac{NH}{CH}&=\dfrac{\overline{\Delta}NBD}{\overline{\Delta}CBD}\\&=\dfrac{\overline{\Delta}FBD-\overline{\Delta}FBN}{\overline{\Delta}CBD}\\&=\dfrac{FB\cdot FD-FB\cdot FN}{CB\cdot CD}\\&=\dfrac{FB\cdot ND}{CB\cdot CD}\\&=\dfrac{FB}{CB}\cdot \dfrac{EN}{EF},\end{split}\]所以$$\dfrac{EN\cdot BF}{EF\cdot BC}\cdot \dfrac{CH}{NH}=1,$$即 ④ 成立，从而 ① 成立，故结论得证
答案
解析
备注
