如图,双曲线的中心在坐标原点 $O$,焦点在 $x$ 轴上,两条渐近线分别为 $l_1,l_2$,经过右焦点 $F$ 垂直于 $l_1$ 的直线分别交 $l_1,l_2$ 于 $A,B$ 两点.又已知该双曲线的离心率 $e=\dfrac{\sqrt 5}{2}$.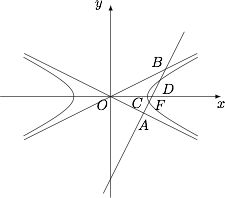

【难度】
【出处】
2009年全国高中数学联赛四川省预赛
【标注】
-
求证:$\left|\overrightarrow{OA}\right|,\left|\overrightarrow{AB}\right|,\left|\overrightarrow{OB}\right|$ 依次成等差数列;标注答案略解析由已知 $e^2=\dfrac 54$,即$$\dfrac{c^2}{a^2}=\dfrac 54,$$故$$a^2=\dfrac 45 c^2 \cdots \text{ ① }$$从而$$b^2=c^2-a^2=\dfrac 15 c^2,\cdots \text{ ② }$$所以$$\dfrac ba=\dfrac{\dfrac c{\sqrt 5}}{\dfrac{2c}{\sqrt 5}}=\dfrac 12.$$设 $\angle{AOF}=\angle{BOF}=\theta$,则 $\tan \theta =\dfrac 12$,所以$$\tan \angle{AOB}=\tan{2\theta}=\dfrac{2\tan \theta}{1-\tan^2 \theta}=\dfrac 43,$$即 $\dfrac{\left|\overrightarrow{AB}\right|}{\left|\overrightarrow{OA}\right|}=\dfrac 43$.
令 $\left|\overrightarrow{OA}\right|=3m$($m>0$),则 $\left|\overrightarrow{AB}\right|=4m$,$\left|\overrightarrow{OB}\right|=5m$,满足$$\left|\overrightarrow{OA}\right|+\left|\overrightarrow{OB}\right|=2\left|\overrightarrow{AB}\right|.$$所以,$\left|\overrightarrow{OA}\right|$,$\left|\overrightarrow{AB}\right|$,$\left|\overrightarrow{OB}\right|$ 依次成等差数列. -
若 $F(\sqrt 5,0)$,求直线 $AB$ 在双曲线上所截得的弦 $CD$ 的长度.标注答案$\dfrac{4}{3}$解析由已知 $c^2=5$,代入 ①,② 得$$a^2=4 , b^2=1,$$于是双曲线的方程为 $\dfrac{x^2}{4}-y^2=1$.
设直线 $AB$ 的斜率为 $k$,则$$k=\tan \angle{AFO}=\cot \theta =2,$$于是直线 $AB$ 的方程为$$y=2(x-\sqrt 5),$$与双曲线方程联立,得$$15x^2-32\sqrt 5x+84=0,$$故弦 $CD$ 的长度\[\begin{split}|CD|&=\sqrt{1+k^2}\cdot \dfrac{\sqrt{\Delta}}{15}\\&=\sqrt 5 \cdot \dfrac{\sqrt{(-32\sqrt 5)^2-4\cdot 15\cdot 84}}{15}\\&=\dfrac 43.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2