已知函数 $f(x)$ 满足 $f(x)=f'(1){\rm e}^{x-1}-f(0)x+\dfrac 12x^2$．
【难度】
【出处】
无
【标注】
-
求 $f(x)$ 的解析式及单调区间；标注答案$f(x)={\rm e}^x-x+\dfrac 12x^2$．
$f(x)$ 的单调递减区间为 $(-\infty,0)$，单调递增区间为 $(0,+\infty)$解析根据题意，有$$f'(x)=f'(1){\rm e}^{x-1}-f(0)+x,$$于是$$\begin{cases} f(0)=f'(1)\cdot {\rm e}^{-1},\\ f'(1)=f'(1)-f(0)+1,\end{cases} $$解得 $f(0)=1$，$f'(1)={\rm e}$，于是$$f(x)={\rm e}^x-x+\dfrac 12x^2,$$进而$$f'(x)={\rm e}^x-1+x,$$而$$f''(x)={\rm e}^x+1>0 , f'(0)=0,$$因此函数 $f(x)$ 在 $(-\infty,0)$ 上单调递减，在 $(0,+\infty)$ 上单调递增． -
若 $f(x)\geqslant \dfrac 12x^2+ax+b$，求 $(a+1)b$ 的最大值．标注答案$\dfrac 12{\rm e}$解析题中不等式即$${\rm e}^x\geqslant (a+1)x+b,$$其几何意义为曲线 $y={\rm e}^x$ 恒在直线 $l:y=(a+1)x+b$ 上方（包括直线上），如图．
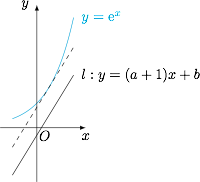容易证明 $a+1\geqslant 0$，于是视 $a+1$ 为定值时，当直线 $l$ 与函数 $y={\rm e}^x$ 的图象相切时 $(a+1)b$ 最大．
设切点横坐标为 $t$，则切线方程为$$y={\rm e}^t\cdot x+{\rm e}^t(1-t),$$于是可得 $(a+1)b$ 的最大值即$$\varphi(t)={\rm e}^t\cdot {\rm e}^t(1-t),t\in\mathbb R$$的最大值．
函数 $\varphi(t)$ 的导函数$$\varphi'(t)={\rm e}^{2t}(2t-1),$$于是 $\varphi(t)$ 及极大值，亦为最大值为$$\varphi\left(\dfrac 12\right)=\dfrac 12{\rm e},$$因此所求的最大值为 $\dfrac 12{\rm e}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
