如图,已知圆 $O:x^2+y^2=1$ 与 $x$ 轴交于 $A$,$B$ 两点,与 $y$ 轴交于点 $C$,$M$ 是圆 $O$ 上任一点(除去圆 $O$ 与两坐标轴的交点).直线 $AM$ 与 $BC$ 交于点 $P$,直线 $CM$ 与 $x$ 轴交于点 $N$,设直线 $PM$,$PN$ 的斜率分别为 $m$,$n$,求证:$m-2n$ 为定值.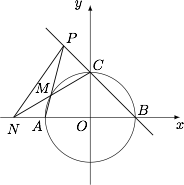

【难度】
【出处】
2014年全国高中数学联赛陕西省预赛(二试)
【标注】
【答案】
略
【解析】
设 $M(x_0,y_0)$($x_0 \neq 0,\pm 1$),则$$x_0^2+y_0^2=1 , m=\dfrac {y_0}{x_0+1},$$所以直线 $AM$ 的方程为$$y=\dfrac {y_0}{x_0+1}(x+1),$$与直线 $BC$ 的方程 $x+y=1$ 联立,求得点 $P$ 的坐标为$$ \left(\dfrac {1+x_0-y_0}{1+x_0+y_0}, \dfrac {2y_0}{1+x_0+y_0}\right).$$由 $C(0,1)$,$M (x_0,y_0)$,$N(x,0)$ 三点共线,可得$$N\left(\dfrac {x_0}{1-y_0},0\right),$$所以\[\begin{split}n&=k_{PN}=\dfrac {\dfrac {2y_0}{1+x_0+y_0}-0}{\dfrac {1+x_0-y_0}{1+x_0+y_0}-\dfrac {x_0}{1-y_0}}\\&=-\dfrac {1-y_0}{1+x_0-y_0},\end{split}\]故\[\begin{split}m-2n&= \dfrac {y_0}{1+x_0}+\dfrac {2(1-y_0)}{1+x_0-y_0}\\&=\dfrac {(1+x_0)(2-y_0)-y_0^2}{(1+x_0)(1+x_0-y_0)}=1,\end{split}\]即$$m-2n=1,$$因此 $m-2n$ 为定值.
答案
解析
备注