如图，$AB$ 是 $\odot O$ 的直径，弦 $BD,CA$ 的延长线相交于点 $E$，$EF$ 垂直 $BA$ 的延长线于点 $F$．求证：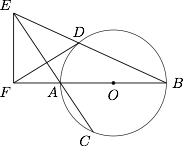
【难度】
【出处】
2009年全国高中数学联赛黑龙江省预赛
【标注】
-
$\angle{DEA}=\angle{DFA}$；标注答案略解析连结 $AD$．
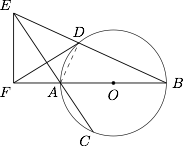因为 $AB$ 为圆的直径，所以$$\angle{ADB}=90^{\circ}.$$又因为$$EF\perp AB , \angle{EFA}=90^{\circ},$$故 $A,D,E,F$ 四点共圆，所以$$\angle{DEA}=\angle{DFA}.$$ -
$AB^2=BE\cdot BD-AE\cdot AC$．标注答案略解析由 $(1)$ 知，$A,D,E,F$ 四点共圆，所以$$BD\cdot BE=BA\cdot BF.$$又因为 $\triangle{ABC}\backsim \triangle{AEF}$，所以$$\dfrac{AB}{AE}=\dfrac{AC}{AF},$$即$$AB\cdot AF=AE\cdot AC,$$故\[\begin{split}&BE\cdot BD-AE\cdot AC\\=&BA\cdot BF-AB\cdot AF\\=&AB(BF-AF)\\=&AB^2.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
