为了解某校高三学生的视力情况,随机抽查了该校 $100$ 名高三学生的视力情况,得到频率分布直方图如图.由于不慎将部分数据丢失,但知道前 $4$ 组的频数从左到右依次是等比数列 $\{a_n\}$ 的前四项,后 $6$ 组的频数从左到右依次是等差数列 $\{b_n\}$ 的前六项.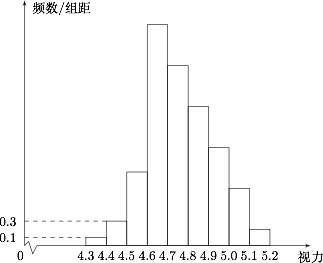

【难度】
【出处】
2009年全国高中数学联赛黑龙江省预赛
【标注】
-
求等比数列 $\{a_n\}$ 的通项公式;标注答案$a_n=3^{n-1}$解析由题意知$$\begin{split}a_1&=0.1\cdot 0.1 \cdot 100=1,\\a_2&=0.3\cdot 0.1 \cdot 100=3,\end{split}$$因此数列 $\{a_n\}$ 是一个首项为 $1$,公比为 $3$ 的等比数列,所以$$a_n=3^{n-1}.$$
-
求最大频率;标注答案$0.27$解析最大频率为 $\dfrac {27}{100}=0.27$.
-
设 $\dfrac{c_1}{a_1}+\dfrac{c_2}{a_2}+\cdots +\dfrac{c_n}{a_n}=b_{n+1}$($n\in \mathbb N^*$),求数列 $\{c_n\}$ 前 $2007$ 项的和 $S_{2007}$.标注答案$\dfrac{5(1-3^{2007})}{2}+27$解析因为 $b_1=a_4=27$,且\[\begin{split}b_1+b_2+\cdots +b_6&=100-(a_1+a_2+a_3)\\&=100-(1+3+9)\\&=87\\&=6b_1+\dfrac{6\cdot 5}{2}d,\end{split}\]解得 $d=-5$,因此数列 $\{b_n\}$ 是首项为 $27$,公差为 $-5$ 的等差数列,所以$$b_n=32-5n.$$又\[\dfrac{c_n}{a_n}=b_{n+1}-b_n=-5,\]所以$$c_n=-5a_n=-5\cdot 3^{n-1}(n\in {\mathbb N}^*,n\geqslant 2).$$又因为$$\dfrac{c_1}{a_1}=b_2=22 , c_1=22,$$因此数列 $\{c_n\}$ 是一个从第 $2$ 项开始的公比为 $3$ 的等比数列,所以$$S_{2007}=\dfrac{5(1-3^{2007})}{2}+27.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3