如图,抛物线 $y^2=2x$ 及点 $P(1,1)$,过点 $P$ 的不重合的直线 $l_1,l_2$ 与此抛物线分别交于点 $A,B,C,D$.证明:$A,B,C,D$ 四点共圆的充要条件是直线 $l_1$ 与 $l_2$ 的倾斜角互补.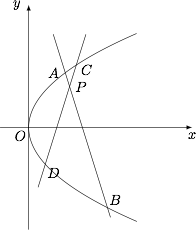

【难度】
【出处】
2009年全国高中数学联赛江苏省复赛
【标注】
【答案】
略
【解析】
必要性:
设 $l_1,l_2$ 的切斜角分别为 $\alpha ,\beta$,由题设知 $\alpha ,\beta \in(0,\pi)$.
易知直线 $l_1$ 的参数方程为$$\begin{cases}x=1+t\cos \alpha ,\\ y=1+t\sin \alpha,\end{cases}$$代入抛物线方程可化得$$t^2 \sin^2 \alpha +2(\sin \alpha -\cos \alpha)t-1=0.$$设上述方程的两根为 $t_1,t_2$,则$$t_1t_2=\dfrac{-1}{\sin^2 \alpha}.$$由参数 $t$ 的几何意义,得$$AP\cdot BP=\dfrac 1{\sin^2\alpha}.$$同理$$CD\cdot DP=\dfrac 1{\sin^2 \beta}.$$若 $A,B,C,D$ 四点共圆,则$$AP\cdot BP=CP\cdot DP,$$即$$\sin^2 \alpha=\sin^2 \beta.$$因为 $\alpha ,\beta \in (0,\pi)$,所以$$\sin \alpha =\sin \beta.$$又 $l_1,l_2$ 不重合,则 $\alpha \ne \beta$,所以 $\alpha+\beta =\pi$.
充分性:
若 $\alpha +\beta =\pi$,因为 $\alpha ,\beta \in(0,\pi)$,故$$\sin \alpha =\sin \beta , \alpha \ne 0 , \beta\ne 0,$$所以$$\dfrac 1{\sin^2 \alpha}=\dfrac 1{\sin^2 \beta},$$即$$AP\cdot BP=CP\cdot DP,$$故 $A,B,C,D$ 四点共圆.
设 $l_1,l_2$ 的切斜角分别为 $\alpha ,\beta$,由题设知 $\alpha ,\beta \in(0,\pi)$.
易知直线 $l_1$ 的参数方程为$$\begin{cases}x=1+t\cos \alpha ,\\ y=1+t\sin \alpha,\end{cases}$$代入抛物线方程可化得$$t^2 \sin^2 \alpha +2(\sin \alpha -\cos \alpha)t-1=0.$$设上述方程的两根为 $t_1,t_2$,则$$t_1t_2=\dfrac{-1}{\sin^2 \alpha}.$$由参数 $t$ 的几何意义,得$$AP\cdot BP=\dfrac 1{\sin^2\alpha}.$$同理$$CD\cdot DP=\dfrac 1{\sin^2 \beta}.$$若 $A,B,C,D$ 四点共圆,则$$AP\cdot BP=CP\cdot DP,$$即$$\sin^2 \alpha=\sin^2 \beta.$$因为 $\alpha ,\beta \in (0,\pi)$,所以$$\sin \alpha =\sin \beta.$$又 $l_1,l_2$ 不重合,则 $\alpha \ne \beta$,所以 $\alpha+\beta =\pi$.
充分性:
若 $\alpha +\beta =\pi$,因为 $\alpha ,\beta \in(0,\pi)$,故$$\sin \alpha =\sin \beta , \alpha \ne 0 , \beta\ne 0,$$所以$$\dfrac 1{\sin^2 \alpha}=\dfrac 1{\sin^2 \beta},$$即$$AP\cdot BP=CP\cdot DP,$$故 $A,B,C,D$ 四点共圆.
答案
解析
备注