• 知识点

  >

  微积分初步

  >

  利用导数研究函数的性质

  >

  利用导数研究函数的单调性

当 $a\leqslant 0$ 时，$f(x)$ 在 $\mathbb R$ 上单调递减；
当 $a>0$ 时，$f(x)$ 在 $\left(-\infty,\ln\dfrac{1}{a}\right)$ 上单调递减，在 $\left(\ln\dfrac{1}{a},+\infty\right)$ 上单调递增

函数 $f(x)$ 的导函数为\[f'(x)=2a{\rm e}^{2x}+(a-2){\rm e}^{x}-1=(a{\rm e}^{x}-1)(2{\rm e}^{x}+1).\]当 $a\leqslant 0$ 时，$f'(x)<0$；
当 $a>0$ 时，在区间 $\left(-\infty,\ln\dfrac{1}{a}\right)$ 上有 $f'(x)<0$，在区间 $\left(\ln\dfrac{1}{a},+\infty\right)$ 上有 $f'(x)>0$．
综上，当 $a\leqslant 0$ 时，$f(x)$ 在 $\mathbb R$ 上单调递减；
当 $a>0$ 时，$f(x)$ 在 $\left(-\infty,\ln\dfrac{1}{a}\right)$ 上单调递减，在 $\left(\ln\dfrac{1}{a},+\infty\right)$ 上单调递增．

• 知识点

  >

  微积分初步

  >

  利用导数研究函数的性质

  >

  利用导数研究函数的零点
• 方法

  >

  代数处理

  >

  分离变量法

$(0,1)$

令 $f(x)=0$，即 $a{\rm e}^{2x}+(a-2){\rm e}^{x}-x=0$，所以有\[a=\dfrac{2{\rm e}^{x}+x}{{\rm e}^{2x}+{\rm e}^{x}}.\]于是函数 $f(x)$ 有两个零点，即 $y=a$ 与 $g(x)=\dfrac{2{\rm e}^{x}+x}{{\rm e}^{2x}+{\rm e}^{x}}$ 的图象有两个公共点．
函数 $g(x)$ 的导函数为$$g'(x)=-\dfrac{(2{\rm e}^{x}+1)({\rm e}^{x}+x-1)}{{\rm e}^{x}({\rm e}^{x}+1)^{2}},$$当 $x<0$ 时，$g'(x)>0$；当 $x>0$ 时，$g'(x)<0$ 时，所以 $g(x)$ 在 $(-\infty,0)$ 上单调递增，在 $(0,+\infty)$ 上单调递减，且 $g(x)$ 在 $x=0$ 处取得最大值 $g(0)=1$，结合\[\lim\limits_{x\to -\infty}g(x)=-\infty,\lim\limits_{x\to +\infty}g(x)=0,\]函数 $g(x)$ 的图象如图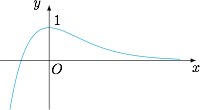．情形一当 $a\geqslant 1$ 时，$y=a$ 与 $g(x)$ 至多有一个公共点，不符合题意；
情形二当 $a\leqslant 0$ 时，由于当 $x\geqslant 0$ 时，$g(x)>0$，而当 $x<0$ 时，$g(x)$ 单调递增，所以 $y=a$ 与 $g(x)$ 至多有一个公共点，不符合题意；
情形三当 $0<a<1$ 时，一方面，由于\[g(-2)<0<a,g(0)=1>a,\]且 $g(x)$ 在 $(-2,0)$ 上单调递增，所以 $y=a$ 与 $g(x)$ 在 $(-2,0)$ 上有且仅有一个公共点．
另一方面，取 $x_{0}=\ln \dfrac{3}{a}$，\[g(x_{0})=\dfrac{2{\rm e}^{x_{0}}+x_{0}}{{\rm e}^{2x_{0}}+{\rm e}^{x_{0}}}<\dfrac{3{\rm e}^{x_{0}}}{{\rm e}^{2x_{0}}}=\dfrac{3}{{\rm e}^{x_{0}}}=a,\]所以在 $\left(0,\ln \dfrac{3}{a}\right)$ 上，有\[g(0)>a, g\left(\ln \dfrac{3}{a}\right)<a.\]且 $g(x)$ 在区间 $\left(0,\ln \dfrac{3}{a}\right)$ 上单调递减，于是 $y=a$ 与 $g(x)$ 在区间 $\left(0,\ln \dfrac{3}{a}\right)$ 上有且仅有一个交点．
综上，当 $0<a<1$ 时，函数 $f(x)$ 有两个零点．