如图，在锐角三角形 $ABC$ 中，$\angle BAC \neq 60^{\circ}$，过点 $B$，$C$ 分别作三角形 $ABC$ 的外接圆的切线 $BD$，$CE$，且满足 $BD=CE=BC$．直线 $DE$ 与 $AB$，$AC$ 的延长线分别交于点 $F$，$G$．设 $CF$ 与 $BD$ 交于点 $M$，$CE$ 与 $BG$ 交于点 $N$．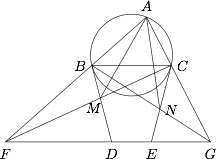
证明：$AM=AN$．
证明：$AM=AN$．【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图，设两条切线 $BD$，$CE$ 交于点 $K$，则 $BK=CK$．结合 $BD=CE$ 可知 $DE \parallel BC$．作 $\angle BAC$ 的平分线 $AL$ 交 $BC$ 于点 $L$，连结 $LM$，$LN$．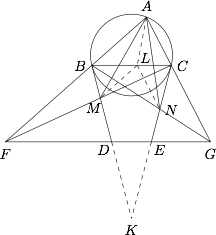
由 $DE \parallel BC$ 知，$$\angle ABC=\angle DFB , \angle FDB=\angle DBC=\angle BAC,$$故 $\triangle ABC$ 与 $\triangle DFB$ 相似．
由此并结合 $DE \parallel BC$，$BD=CB$ 及内角平分线定理可得$$\dfrac {MC}{MF}=\dfrac {BC}{FD}=\dfrac {BD}{FD}=\dfrac {AC}{AB}=\dfrac {LC}{LB},$$因此 $LM \parallel BF$．
同理，$LN \parallel CG$．
由此推出\[\begin{split}\angle ALM&= \angle ALB+\angle BLM\\&=\angle ALB+\angle ABL\\&=180^{\circ}-\angle BAL\\&=180^{\circ}-\angle CAL\\&= \angle ALC+\angle ACL\\&=\angle ALC+\angle CLN\\&=\angle ALN,\end{split}\]再结合 $BC \parallel FG$ 及内角平分线定理可得\[\begin{split} \dfrac {LM}{LN}&=\dfrac {LM}{BF}\cdot \dfrac {BF}{CG}\cdot \dfrac {CG}{LN}\\&=\dfrac {CL}{BC}\cdot \dfrac {AB}{AC}\cdot \dfrac {BC}{BL}\\&=\dfrac {LC}{LB}\cdot \dfrac {AB}{AC}=1,\end{split}\]即 $LM=LN$．
故由$$AL=AL , \angle ALM=\angle ALN , LM=LN,$$得到 $\triangle ALM$ 与 $\triangle ALN$ 全等，因而 $AM=AN$，证毕．
由 $DE \parallel BC$ 知，$$\angle ABC=\angle DFB , \angle FDB=\angle DBC=\angle BAC,$$故 $\triangle ABC$ 与 $\triangle DFB$ 相似．由此并结合 $DE \parallel BC$，$BD=CB$ 及内角平分线定理可得$$\dfrac {MC}{MF}=\dfrac {BC}{FD}=\dfrac {BD}{FD}=\dfrac {AC}{AB}=\dfrac {LC}{LB},$$因此 $LM \parallel BF$．
同理，$LN \parallel CG$．
由此推出\[\begin{split}\angle ALM&= \angle ALB+\angle BLM\\&=\angle ALB+\angle ABL\\&=180^{\circ}-\angle BAL\\&=180^{\circ}-\angle CAL\\&= \angle ALC+\angle ACL\\&=\angle ALC+\angle CLN\\&=\angle ALN,\end{split}\]再结合 $BC \parallel FG$ 及内角平分线定理可得\[\begin{split} \dfrac {LM}{LN}&=\dfrac {LM}{BF}\cdot \dfrac {BF}{CG}\cdot \dfrac {CG}{LN}\\&=\dfrac {CL}{BC}\cdot \dfrac {AB}{AC}\cdot \dfrac {BC}{BL}\\&=\dfrac {LC}{LB}\cdot \dfrac {AB}{AC}=1,\end{split}\]即 $LM=LN$．
故由$$AL=AL , \angle ALM=\angle ALN , LM=LN,$$得到 $\triangle ALM$ 与 $\triangle ALN$ 全等，因而 $AM=AN$，证毕．
答案
解析
备注
