直线 $l$ 是椭圆 $\dfrac{x^{2}}{4}+\dfrac{y^{2}}{3}=1$ 的左准线，$F_{1}$ 是左焦点，动点 $P$ 在 $l$ 上运动，以线段 $PF_{1}$ 为一边的正三角形的第三个顶点为 $M$，且 $P,F_{1},M$ 三点逆时针排列，求点 $M$ 的轨迹方程．
【难度】
【出处】
2008年全国高中数学联赛河南省预赛
【标注】
【答案】
$x-\sqrt 3y+7=0$
【解析】
设 $l$ 与 $x$ 轴交于点 $P_{0}$，当点 $P$ 在点 $P_{0}$ 位置时，点 $M$ 的位置在点 $M_{0}$ 处．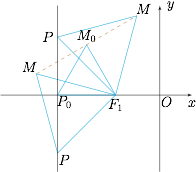
当点 $P$ 在点 $P_{0}$ 上方时，点 $M$ 的位置在 $M_{0}$ 的右上方．
由于$$\begin{split}\angle PF_{1}M&=\angle P_{0}F_{1}M_{0},\\\angle PF_{1}P_{0}&=\angle M_{0}F_{1}M,\\P_{0}F_{1}&=M_{0}F_{1},\\PF_{1}&=MF_{1},\end{split}$$所以\[\triangle PF_{1}P_{0}\cong \triangle MF_{1}M_{0},\]可知\[\angle PP_{0}F_{1}=\angle MM_{0}F_{1}=90^{\circ},\]即 $MM_{0}\perp M_{0}F_{1}$．
当点 $P$ 在 $P_{0}$ 下方时，点 $M$ 在点 $M_{0}$ 的左下方．
同理可证 $MM_{0}\perp M_{0}F_{1}$．
因此$$F_{1}(-1,0),M\left(-\dfrac{5}{2}, \dfrac{3\sqrt 3}{2}\right), k_{M_{0}F_{1}}=-\sqrt 3,$$故 $M$ 的轨迹方程为\[y-\dfrac{3\sqrt 3}{2}=\dfrac{\sqrt 3}{3}\left(x+\dfrac{5}{2}\right),\]即 $x-\sqrt 3y+7=0$．
当点 $P$ 在点 $P_{0}$ 上方时，点 $M$ 的位置在 $M_{0}$ 的右上方．由于$$\begin{split}\angle PF_{1}M&=\angle P_{0}F_{1}M_{0},\\\angle PF_{1}P_{0}&=\angle M_{0}F_{1}M,\\P_{0}F_{1}&=M_{0}F_{1},\\PF_{1}&=MF_{1},\end{split}$$所以\[\triangle PF_{1}P_{0}\cong \triangle MF_{1}M_{0},\]可知\[\angle PP_{0}F_{1}=\angle MM_{0}F_{1}=90^{\circ},\]即 $MM_{0}\perp M_{0}F_{1}$．
当点 $P$ 在 $P_{0}$ 下方时，点 $M$ 在点 $M_{0}$ 的左下方．
同理可证 $MM_{0}\perp M_{0}F_{1}$．
因此$$F_{1}(-1,0),M\left(-\dfrac{5}{2}, \dfrac{3\sqrt 3}{2}\right), k_{M_{0}F_{1}}=-\sqrt 3,$$故 $M$ 的轨迹方程为\[y-\dfrac{3\sqrt 3}{2}=\dfrac{\sqrt 3}{3}\left(x+\dfrac{5}{2}\right),\]即 $x-\sqrt 3y+7=0$．
答案
解析
备注
