正四棱锥 $P-ABCD$ 中 $AB=3$，且侧面 $PAD$ 与侧面 $CPD$ 所成二面角大小为 $\dfrac{2\pi}{3}$．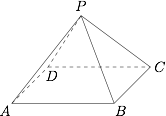
【难度】
【出处】
2008年全国高中数学联赛河南省预赛
【标注】
-
求证：平面 $PAD\perp \text{平面}PBC$；标注答案略解析由于 $P-ABCD$ 是正四棱锥，分别过 $C,A$ 作 $PD$ 的垂线，则垂线必交于 $PD$ 上一点 $Q$，则 $\angle AQC=\dfrac{2\pi}{3}$，且 $AQ=CQ$．
又因为$$AC=\sqrt 2AB=3\sqrt 2,$$所以\[\begin{split}AQ&=CQ=\dfrac{AC}{\sin 120^{\circ}}\cdot \sin \dfrac{180^{\circ}-120^{\circ}}{2}=\sqrt 6,\\DQ&=\sqrt{CD^{2}-CQ^{2}}=\sqrt 3.\end{split}\]
设 $PD=x$，过点 $P$ 作 $PE\perp AD$ 于点 $E$，$PF\perp BC$ 于点 $F$．
由 $PQ^{2}=PC^{2}-CQ^{2}$，得 $x=\dfrac{3\sqrt 3}{2}$．
由于\[\begin{split}PE&=PF\\&=\sqrt{PD^{2}-\left(\dfrac{AB}{2}\right)^{2}}\\&=\sqrt{\left(\dfrac{3\sqrt 3}{2}\right)^{2}-\left(\dfrac{3}{2}\right)^{2}}\\&=\dfrac{3\sqrt 2}{2},\end{split}\]所以\[PE^{2}+PF^{2}=9=EF^{2},\]故 $PE\perp PF$．
又因为$$PE\perp AD , AD\parallel BC,$$从而$$PE\perp CB , PE\perp \text{平面}PCB,$$故平面 $PAD\perp \text{平面}PCB$． -
判断该四棱锥是否存在外接球，若存在，求出该四棱锥外接球的体积；若不存在，请说明理由．标注答案存在，体积为 $\dfrac{243\pi}{16}$解析设 $O$ 为正方形 $ABCD$ 的中心，则四棱锥外接球的球心 $O'$ 必在直线 $PO$ 上，$$PO=\sqrt{PA^{2}-AO^{2}}=\dfrac{3}{2}.$$设 $OO'=x$，$O'$ 在四棱锥内部时，$O'P^{2}=O'A^{2}$ 等价于\[(PO-OO')^{2}=O'O^{2}+OA^{2},\]解得 $x=-\dfrac{3}{4}<0$，舍去．
因此 $O'$ 在四棱锥外部，$$O'P^{2}=O'A^{2},$$即\[(PO+O'O)^{2}=O'O^{2}+OA^{2},\]所以\[\left(\dfrac{3}{2}+OO'\right)^{2}=OO'^{2}+\dfrac{AC^{2}}{4},\]因此\[3OO'+\dfrac{9}{4}=\dfrac{9}{2},\]解得 $OO'=\dfrac{3}{4}$，则\[R=OO'+PO=\dfrac{9}{4},\]可知$$V_{\text{球}}=\dfrac{4}{3}\pi R^{3}=\dfrac{243}{16}\pi.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
