已知函数 $f(x)=|\sin x|$ 的图象与直线 $y=kx$（$k>0$）有且仅有三个公共点，公共点的横坐标的最大值为 $\alpha$．求证：$\dfrac {\cos \alpha}{\sin \alpha+\sin 3\alpha}=\dfrac {1+\alpha^2}{4\alpha}$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图．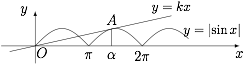
$f(x)=|\sin x|$ 的图象与直线 $y=kx$（$k>0$）有三个公共点，且在 $\left(\pi,\dfrac {3\pi}{2}\right)$ 内相切，其切点为 $A(\alpha,-\sin \alpha)$，$\alpha \in \left(\pi,\dfrac {3\pi}{2}\right)$．
由于$$f'(x)=-\cos x, x \in \left(\pi,\dfrac {3\pi}{2}\right),$$所以$$-\cos \alpha=-\dfrac {\sin \alpha}{\alpha},$$即 $\alpha=\tan \alpha$，因此\[\begin{split}\dfrac {\cos \alpha}{\sin \alpha+\sin 3\alpha}&=\dfrac {\cos \alpha}{2\sin 2\alpha\cos \alpha}\\&= \dfrac {1}{4\sin \alpha \cos \alpha}\\&=\dfrac {\sin ^2\alpha +\cos ^2\alpha}{4\sin \alpha \cos \alpha}\\&=\dfrac {1+\tan^2 \alpha}{4\tan \alpha} \\&=\dfrac {1+\alpha^2}{4\alpha}.\end{split}\]
$f(x)=|\sin x|$ 的图象与直线 $y=kx$（$k>0$）有三个公共点，且在 $\left(\pi,\dfrac {3\pi}{2}\right)$ 内相切，其切点为 $A(\alpha,-\sin \alpha)$，$\alpha \in \left(\pi,\dfrac {3\pi}{2}\right)$．由于$$f'(x)=-\cos x, x \in \left(\pi,\dfrac {3\pi}{2}\right),$$所以$$-\cos \alpha=-\dfrac {\sin \alpha}{\alpha},$$即 $\alpha=\tan \alpha$，因此\[\begin{split}\dfrac {\cos \alpha}{\sin \alpha+\sin 3\alpha}&=\dfrac {\cos \alpha}{2\sin 2\alpha\cos \alpha}\\&= \dfrac {1}{4\sin \alpha \cos \alpha}\\&=\dfrac {\sin ^2\alpha +\cos ^2\alpha}{4\sin \alpha \cos \alpha}\\&=\dfrac {1+\tan^2 \alpha}{4\tan \alpha} \\&=\dfrac {1+\alpha^2}{4\alpha}.\end{split}\]
答案
解析
备注
