查看数据源：599165b52bfec200011dde35
设函数 $f\left(x\right) = \dfrac{1}{x}$，$g\left(x\right) = - {x^2} + bx$．若 $y = f\left(x\right)$ 的图象与 $y = g\left(x\right)$ 的图象有且仅有两个不同的公共点 $A\left({x_1} , {y_1}\right)$，$B\left({x_2} , {y_2}\right)$，则下列判断正确的是 \((\qquad)\)
A: ${x_1} + {x_2} > 0 , {y_1} + {y_2} > 0$
B: ${x_1} + {x_2} > 0 , {y_1} + {y_2} < 0$
C: ${x_1} + {x_2} < 0 , {y_1} + {y_2} > 0$
D: ${x_1} + {x_2} < 0 , {y_1} + {y_2} < 0$
【难度】
【出处】
2012年高考山东卷（文）
【标注】
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的零点
  • 方法
    >
    代数处理
    >
    半分离变量法
【答案】
B
【解析】
考虑方程$$-x+b=\dfrac{1}{x^2},$$于是直线 $y=-x+b$ 与幂函数 $y=x^{-2}$ 的图象有两个公共点，如图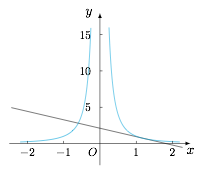．此时有 $x_1+x_2>0$，而$$y_1+y_2=\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1x_2}<0,$$因此正确的答案是 B．
题目 答案 解析 备注
0.134616s