如图，在三棱锥 $P-ABC$ 中，$PB=PC$，$\angle APB=\angle APC=90^{\circ}$，$\angle BPC=60^{\circ}$．若此三棱锥的体积为定值 $V$，求点 $P$ 到平面 $ABC$ 距离的最大值．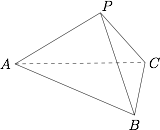
【难度】
【出处】
2010年全国高中数学联赛山东省预赛
【标注】
【答案】
$\sqrt [3]{2V}$
【解析】
如图，因为$$PB=PC , \angle APB=\angle APC=90^{\circ} , PA=PA,$$所以$$\triangle PAB \cong \triangle PAC,$$故 $AB=AC$．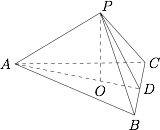
设 $BC$ 的中点为 $D$，连结 $AD$，$PD$，则$$AD \perp BC , PD \perp BC,$$故$$BC \perp \text{ 平面}PAD , \text{平面}PAD \perp \text{平面}ABC.$$作 $PO \perp AD$，垂足为 $O$，则 $PO \perp \text{ 平面}ABC$．
设 $PO=h$，$\angle PAD =\alpha$（$0^{\circ}< \alpha <90^{\circ}$），则$$PA =\dfrac {PO}{\sin \angle PAD}=\dfrac {h}{\sin \alpha}.$$因为 $\angle APB =\angle APC=90^{\circ}$，所以$$PA\perp \text{ 平面}PBC , PA \perp PD,$$于是$$PD=PA \cdot \tan \angle PAD=\dfrac {h}{\cos \alpha}.$$因为 $PB=PC$，$\angle BPC=60^{\circ}$，所以 $\triangle PBC$ 是正三角形．
又 $PD \perp BC$，则$$BC=2PD \cot \angle PBD =\dfrac {2h}{\sqrt 3\cos \alpha},$$故$$S_{\triangle PAD}=\dfrac 12PA \cdot PD=\dfrac {h^2}{2\sin \alpha \cos \alpha},$$所以\[\begin{split}V &=\dfrac 13 \cdot S_{\triangle PAD}\cdot BC\\&=\dfrac 13 \cdot \dfrac {h^2}{2\sin \alpha \cos \alpha}\cdot \dfrac {2h}{\sqrt 3\cos \alpha} \\&=\dfrac { h^3}{3\sqrt 3 \sin \alpha\cos^2 \alpha},\end{split}\]因此$$h^3=3\sqrt 3 V \sin \alpha\cos^2 \alpha= 3\sqrt 3 V (\sin \alpha -\sin ^3\alpha).$$设 $t=\sin \alpha$（$0<t<1$），则$$\begin{split}&f(t)=t-t^3,\\&f'(t)=1-3t^2.\end{split}$$令 $f'(t)=0$，得 $t=\dfrac {\sqrt 3}{3}$．
当 $0<t<\dfrac {\sqrt 3}{3}$ 时，$f'(t)>0$；
当 $\dfrac {\sqrt 3}{3}<t<1$ 时，$f'(t)<0$，所以 $t=\dfrac {\sqrt 3}{3}$ 时，$f(t)$ 取得最大值 $\dfrac {2\sqrt 3}{9}$．
因此，$h$ 的最大值为 $\sqrt [3]{2V}$．
设 $BC$ 的中点为 $D$，连结 $AD$，$PD$，则$$AD \perp BC , PD \perp BC,$$故$$BC \perp \text{ 平面}PAD , \text{平面}PAD \perp \text{平面}ABC.$$作 $PO \perp AD$，垂足为 $O$，则 $PO \perp \text{ 平面}ABC$．设 $PO=h$，$\angle PAD =\alpha$（$0^{\circ}< \alpha <90^{\circ}$），则$$PA =\dfrac {PO}{\sin \angle PAD}=\dfrac {h}{\sin \alpha}.$$因为 $\angle APB =\angle APC=90^{\circ}$，所以$$PA\perp \text{ 平面}PBC , PA \perp PD,$$于是$$PD=PA \cdot \tan \angle PAD=\dfrac {h}{\cos \alpha}.$$因为 $PB=PC$，$\angle BPC=60^{\circ}$，所以 $\triangle PBC$ 是正三角形．
又 $PD \perp BC$，则$$BC=2PD \cot \angle PBD =\dfrac {2h}{\sqrt 3\cos \alpha},$$故$$S_{\triangle PAD}=\dfrac 12PA \cdot PD=\dfrac {h^2}{2\sin \alpha \cos \alpha},$$所以\[\begin{split}V &=\dfrac 13 \cdot S_{\triangle PAD}\cdot BC\\&=\dfrac 13 \cdot \dfrac {h^2}{2\sin \alpha \cos \alpha}\cdot \dfrac {2h}{\sqrt 3\cos \alpha} \\&=\dfrac { h^3}{3\sqrt 3 \sin \alpha\cos^2 \alpha},\end{split}\]因此$$h^3=3\sqrt 3 V \sin \alpha\cos^2 \alpha= 3\sqrt 3 V (\sin \alpha -\sin ^3\alpha).$$设 $t=\sin \alpha$（$0<t<1$），则$$\begin{split}&f(t)=t-t^3,\\&f'(t)=1-3t^2.\end{split}$$令 $f'(t)=0$，得 $t=\dfrac {\sqrt 3}{3}$．
当 $0<t<\dfrac {\sqrt 3}{3}$ 时，$f'(t)>0$；
当 $\dfrac {\sqrt 3}{3}<t<1$ 时，$f'(t)<0$，所以 $t=\dfrac {\sqrt 3}{3}$ 时，$f(t)$ 取得最大值 $\dfrac {2\sqrt 3}{9}$．
因此，$h$ 的最大值为 $\sqrt [3]{2V}$．
答案
解析
备注
