如图，四边形 $ABCD$ 内接于圆，$P$ 是 $AB$ 的中点，$PE\perp AD,PF\perp BC,PG\perp CD$，$M$ 是线段 $PG$ 和 $EF$ 的交点，求证：$ME=MF$．
【难度】
【出处】
2008年全国高中数学联赛黑龙江省预赛
【标注】
【答案】
略
【解析】
如图．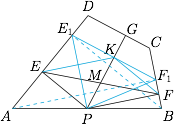
作 $AF_1\perp BC,BE_1\perp AD$，垂足为 $E_1,F_1$，则$$PE_1=\dfrac12AB=PF_1,$$即 $PE_1=PF_1$．
设 $PG\cap E_1F_1=K$，因为 $ABF_1E_1$ 共圆，则$$\angle CF_1E_1=\angle A=\pi-\angle C,$$故$$E_1F_1\parallel CD , PK\perp E_1F_1,$$可得 $K$ 是 $E_1F_1$ 的中点．
因此 $PEKF$ 为平行四边形，易知 $ME=MF$．
作 $AF_1\perp BC,BE_1\perp AD$，垂足为 $E_1,F_1$，则$$PE_1=\dfrac12AB=PF_1,$$即 $PE_1=PF_1$．设 $PG\cap E_1F_1=K$，因为 $ABF_1E_1$ 共圆，则$$\angle CF_1E_1=\angle A=\pi-\angle C,$$故$$E_1F_1\parallel CD , PK\perp E_1F_1,$$可得 $K$ 是 $E_1F_1$ 的中点．
因此 $PEKF$ 为平行四边形，易知 $ME=MF$．
答案
解析
备注
