如图，在凸四边形 $ABCD$ 中，$\angle ABC=\angle ADC$，$E$，$F$，$G$，$H$ 分别为 $AC$，$BD$，$AD$，$CD$ 的中点．求证：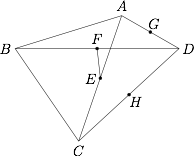
【难度】
【出处】
2010年全国高中数学联赛陕西省预赛（二试）
【标注】
-
$E$，$F$，$G$，$H$ 四点共圆；标注答案略解析连结 $EG$，$EH$，$FG$，$FH$，$GH$，则$$FG \parallel BA , FH \parallel BC,$$所以 $\angle GFH=\angle ABC $．
同理 $\angle GHF=\angle ACB$．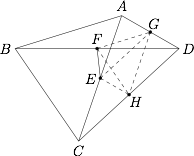
又因为四边形 $DGEH$ 为平行四边形，所以$$\angle GEH=\angle ADC=\angle ABC=\angle GFH,$$所以 $E$，$F$，$G$，$H$ 四点共圆． -
$\angle AEF=\angle ACB-\angle ACD$．标注答案略解析因为 $E$，$F$，$G$，$H$ 四点共圆，所以$$\angle GEF=\angle GHF=\angle ACB.$$又 $EG \parallel CD$，所以 $\angle AEG=\angle ACD$，故$$\angle AEF=\angle GEF-\angle AEG=\angle ACB-\angle ACD.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
