圆心为 $I$ 的 $\triangle ABC$ 的内切圆分别切边 $AC$，$AB$ 于点 $E$，$F$．设 $M$ 为线段 $EF$ 上一点，证明：$\triangle MAB$ 与 $\triangle MAC$ 面积相等的充分必要条件是 $MI \perp BC$．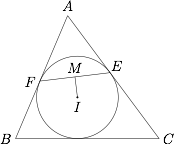
【难度】
【出处】
2010年全国高中数学联赛江苏省复赛（加试）
【标注】
【答案】
略
【解析】
过点 $M$ 作 $MP\perp AC$，$MQ\perp AB$，垂足分别为 $P$，$Q$．
圆 $I$ 切边 $BC$ 于点 $D$，则$$ID\perp BC , IF \perp AB , IE\perp AC.$$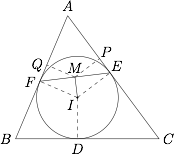
显然 $AF=AE$，所以 $\angle AFM =\angle AEM $，从而推知$$\mathrm {Rt}\triangle QFM \backsim \mathrm {Rt}\triangle PEM,$$得 $\dfrac {MQ}{MP}=\dfrac {MF}{ME}$．
又因为\[\begin{split}\dfrac {S_{\triangle MAB}} {S_{\triangle MAC}}&=\dfrac {\dfrac 12 MQ \cdot AB}{\dfrac 12 MP \cdot AC}\\&=\dfrac {MQ}{MP}\cdot \dfrac {AB}{AC}\\&=\dfrac {MF}{ME}\cdot \dfrac {AB}{AC},\end{split}\]所以 $\triangle MAB$ 与 $\triangle MAC$ 面积相等的充分必要条件是$$ \dfrac {AB}{AC}=\dfrac {ME}{MF}.\quad \cdots\cdots \text{ ① }$$由 ① 可知，问题转化为证明：$\dfrac {AB}{AC}=\dfrac {ME}{MF}$ 的充分必要条件是 $MI \perp BC$．
首先证明：若 $MI \perp BC$，则 $\dfrac {AB}{AC}=\dfrac {ME}{MF}$．
由 $MI \perp BC$ 可知点 $M$ 在直线 $ID$ 上．
因为 $B$，$D$，$I$，$F$ 四点共圆，所以$$\angle MIF=\angle DBF=\angle B,\quad \angle MIE=\angle ECD=\angle C. $$又 $IE=IF$，则由正弦定理得$$\dfrac {MF}{\sin \angle MIF}=\dfrac { FI}{\sin \angle IMF}=\dfrac {IE}{\sin (\pi-\angle IMF)}=\dfrac {ME}{\sin \angle MIE},$$即$$\dfrac {ME}{MF}=\dfrac {\sin C}{\sin B},$$而 $\dfrac {AB}{AC}=\dfrac {\sin C}{\sin B} $，所以$$\dfrac {AB}{AC}=\dfrac {ME}{MF}.$$其次证明：若 $\dfrac {AB}{AC}=\dfrac {ME}{MF}$，则 $MI \perp BC$．
设直线 $ID$ 与 $EF$ 交于点 $M'$，则由上述证明可知 $\dfrac {AB}{AC}=\dfrac {M'E}{M'F} $，从而有 $M \equiv M'$，故命题成立．
圆 $I$ 切边 $BC$ 于点 $D$，则$$ID\perp BC , IF \perp AB , IE\perp AC.$$
显然 $AF=AE$，所以 $\angle AFM =\angle AEM $，从而推知$$\mathrm {Rt}\triangle QFM \backsim \mathrm {Rt}\triangle PEM,$$得 $\dfrac {MQ}{MP}=\dfrac {MF}{ME}$．又因为\[\begin{split}\dfrac {S_{\triangle MAB}} {S_{\triangle MAC}}&=\dfrac {\dfrac 12 MQ \cdot AB}{\dfrac 12 MP \cdot AC}\\&=\dfrac {MQ}{MP}\cdot \dfrac {AB}{AC}\\&=\dfrac {MF}{ME}\cdot \dfrac {AB}{AC},\end{split}\]所以 $\triangle MAB$ 与 $\triangle MAC$ 面积相等的充分必要条件是$$ \dfrac {AB}{AC}=\dfrac {ME}{MF}.\quad \cdots\cdots \text{ ① }$$由 ① 可知，问题转化为证明：$\dfrac {AB}{AC}=\dfrac {ME}{MF}$ 的充分必要条件是 $MI \perp BC$．
首先证明：若 $MI \perp BC$，则 $\dfrac {AB}{AC}=\dfrac {ME}{MF}$．
由 $MI \perp BC$ 可知点 $M$ 在直线 $ID$ 上．
因为 $B$，$D$，$I$，$F$ 四点共圆，所以$$\angle MIF=\angle DBF=\angle B,\quad \angle MIE=\angle ECD=\angle C. $$又 $IE=IF$，则由正弦定理得$$\dfrac {MF}{\sin \angle MIF}=\dfrac { FI}{\sin \angle IMF}=\dfrac {IE}{\sin (\pi-\angle IMF)}=\dfrac {ME}{\sin \angle MIE},$$即$$\dfrac {ME}{MF}=\dfrac {\sin C}{\sin B},$$而 $\dfrac {AB}{AC}=\dfrac {\sin C}{\sin B} $，所以$$\dfrac {AB}{AC}=\dfrac {ME}{MF}.$$其次证明：若 $\dfrac {AB}{AC}=\dfrac {ME}{MF}$，则 $MI \perp BC$．
设直线 $ID$ 与 $EF$ 交于点 $M'$，则由上述证明可知 $\dfrac {AB}{AC}=\dfrac {M'E}{M'F} $，从而有 $M \equiv M'$，故命题成立．
答案
解析
备注
