从双曲线 $\dfrac{x^2}{9}-\dfrac{y^2}{16}=1$ 的左焦点 $F$ 引圆 $x^2+y^2=9$ 的切线，切点为 $T$，延长 $FT$ 交双曲线右支于点 $P$．若 $M$ 为线段 $FP$ 的中点，$O$ 为坐标原点，求 $|MO|-|MT|$ 的值．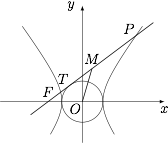
【难度】
【出处】
2008年全国高中数学联赛江苏省复赛
【标注】
【答案】
$1$
【解析】
不妨将点 $P$ 置于第一象限，设 $F'$ 是双曲线的右焦点，连接 $PF'$．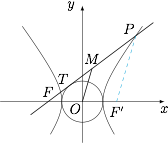
因为 $M,O$ 分别为 $FP$ 与 $FF'$ 的中点，所以$$|MO|=\dfrac12|PF'|.$$由双曲线的定义得$$|PF|-|PF'|=6 , |FT|=\sqrt{|OF|^2-|OT|^2}=4.$$因此有\[\begin{split}|MO|-|MT|&=\dfrac12|PF'|-|MF|+|FT|\\&=\dfrac12\left(|PF'|-|PF|\right)+|FT|\\&=1.\end{split}\]
因为 $M,O$ 分别为 $FP$ 与 $FF'$ 的中点，所以$$|MO|=\dfrac12|PF'|.$$由双曲线的定义得$$|PF|-|PF'|=6 , |FT|=\sqrt{|OF|^2-|OT|^2}=4.$$因此有\[\begin{split}|MO|-|MT|&=\dfrac12|PF'|-|MF|+|FT|\\&=\dfrac12\left(|PF'|-|PF|\right)+|FT|\\&=1.\end{split}\]
答案
解析
备注
