如图，已知 $\triangle ABC$ 的外接圆的直径为 $25$，三条边的长度都是正整数，圆心 $O$ 到边 $AB,BC$ 的距离也都是正整数，$AB>BC$，求 $\triangle ABC$ 三边的长度．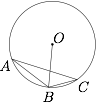
【难度】
【出处】
2008年全国高中数学联赛江苏省复赛
【标注】
【答案】
$15,7,20$
【解析】
如图．
过圆心 $O$ 作 $AB,BC$ 的垂线，垂足为 $D,E$，设$$AB=a,BC=b,OD=d,OE=e,$$其中 $a,b,d,e$ 均为正整数，且 $a>b$，则$$BD=\dfrac{a}{2},BE=\dfrac{b}{2}.$$因为 $DB^2+OD^2=OB^2$，故$$a^2+(2d)^2=25^2,$$同理可得$$b^2+(2e)^2=25^2.$$取不定方程$$x^2+(2y)^2=25^2,$$得两组正整数解$$(x,y)=(15,10),(7,12).$$由 $a>b$，得 $a=15,b=7$，结合$$OD^2=10=OE^2 , OD\perp AB , OE\perp BC,$$所以 $O,D,B,E$ 四点共圆．
由托勒密定理，得$$DE\cdot OB=OD\cdot BE+OE\cdot DB,$$所以 $DE=10$．
由于 $D,E$ 分别是 $AB,AC$ 中点，所以 $DE$ 是 $\triangle ABC$ 的中位线，因此 $AC=20$，即三角形的边长分别为 $15,7,20$．
过圆心 $O$ 作 $AB,BC$ 的垂线，垂足为 $D,E$，设$$AB=a,BC=b,OD=d,OE=e,$$其中 $a,b,d,e$ 均为正整数，且 $a>b$，则$$BD=\dfrac{a}{2},BE=\dfrac{b}{2}.$$因为 $DB^2+OD^2=OB^2$，故$$a^2+(2d)^2=25^2,$$同理可得$$b^2+(2e)^2=25^2.$$取不定方程$$x^2+(2y)^2=25^2,$$得两组正整数解$$(x,y)=(15,10),(7,12).$$由 $a>b$，得 $a=15,b=7$，结合$$OD^2=10=OE^2 , OD\perp AB , OE\perp BC,$$所以 $O,D,B,E$ 四点共圆．由托勒密定理，得$$DE\cdot OB=OD\cdot BE+OE\cdot DB,$$所以 $DE=10$．
由于 $D,E$ 分别是 $AB,AC$ 中点，所以 $DE$ 是 $\triangle ABC$ 的中位线，因此 $AC=20$，即三角形的边长分别为 $15,7,20$．
答案
解析
备注
