如图，已知点 $O$ 为凸四边形 $ABCD$ 内的一点，$AO=OB$，$CO=OD$，$\angle AOB=\angle COD=120^\circ$，点 $E,F,G$ 分别是线段 $AB,BC,CD$ 的中点．求证：$\triangle EFG$ 为正三角形．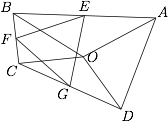
【难度】
【出处】
2008年全国高中数学联赛江苏省复赛（二试）
【标注】
【答案】
略
【解析】
如图．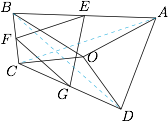
连接 $AC,BD$，则$$EF\parallel AC,EF=\dfrac12AC,FG\parallel BD,FG=\dfrac12BD.$$因为$$OA=OB , OC=OD , \angle AOB=\angle COD=120^\circ,$$所以以 $O$ 为中心，逆时针旋转 $120^\circ$，则 $\triangle AOC$ 成为 $\triangle BOD$，因此 $AC=BD$．
$BD$ 逆时针转到 $AC$ 的角为 $60^\circ$，从而 $EF=FG$，并且 $\angle GFE=60^\circ$，故 $\triangle EFG$ 为正三角形．
连接 $AC,BD$，则$$EF\parallel AC,EF=\dfrac12AC,FG\parallel BD,FG=\dfrac12BD.$$因为$$OA=OB , OC=OD , \angle AOB=\angle COD=120^\circ,$$所以以 $O$ 为中心，逆时针旋转 $120^\circ$，则 $\triangle AOC$ 成为 $\triangle BOD$，因此 $AC=BD$．$BD$ 逆时针转到 $AC$ 的角为 $60^\circ$，从而 $EF=FG$，并且 $\angle GFE=60^\circ$，故 $\triangle EFG$ 为正三角形．
答案
解析
备注
