设 $F$ 是抛物线 $y^{2}=4x$ 的焦点,$A,B$ 为抛物线上异于原点 $O$ 的两点,且满足 $\overrightarrow{FA}\cdot \overrightarrow{FB}=0$.延长 $AF,BF$ 分别交抛物线于点 $C,D$(如图).求四边形 $ABCD$ 面积的最小值.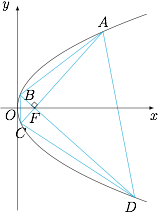

【难度】
【出处】
2008年全国高中数学联赛四川省预赛
【标注】
【答案】
$32$
【解析】
设 $A(x_{1},y_{1}),C(x_{2},y_{2})$.
由题设知,直线 $AC$ 的斜率存在,设为 $k$.
因为直线 $AC$ 过焦点 $F(1,0)$,所以直线 $AC$ 的方程为 $y=k(x-1)$.
联立方程组$$\begin{cases}y=k(x-1),\\ y^{2}=4x,\end{cases}$$消去 $y$ 得\[k^{2}x^{2}-2(k^{2}+2)x+k^{2}=0.\]由根与系数的关系知,\[x_{1}+x_{2}=\dfrac{2k^{2}+4}{k^{2}}, x_{1}x_{2}=1,\]于是\[\begin{split}|AC|&=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\\&=\sqrt{1+k^{2}}\sqrt{(x_{1}+x_{2})^{2}-4x_{1}x_{2}}\\&=\sqrt{1+k^{2}}\sqrt{\left(\dfrac{2k^{2}+4}{k^{2}}\right)^{2}-4}\\&=\dfrac{4(1+k^{2})}{k^{2}}.\end{split}\]又因为 $AC\perp BD$,所以直线 $BD$ 的斜率为 $-\dfrac{1}{k}$,从而直线 $BD$ 的方程为$$y=-\dfrac{1}{k}(x-1).$$同理可求得$$|BD|=4(1+k^{2}).$$故\[\begin{split}S_{ABCD}&=\dfrac{1}{2}\cdot |AC|\cdot |BD|\\&=\dfrac{8(1+k^{2})^{2}}{k^{2}}\\&=8\left(k^{2}+\dfrac{1}{k^{2}}+2\right)\\&\geqslant 8\cdot (2+2)\\&=32,\end{split}\]当 $k=\pm 1$ 时等号成立.
因此四边形 $ABCD$ 的最小面积为 $32$.
由题设知,直线 $AC$ 的斜率存在,设为 $k$.
因为直线 $AC$ 过焦点 $F(1,0)$,所以直线 $AC$ 的方程为 $y=k(x-1)$.
联立方程组$$\begin{cases}y=k(x-1),\\ y^{2}=4x,\end{cases}$$消去 $y$ 得\[k^{2}x^{2}-2(k^{2}+2)x+k^{2}=0.\]由根与系数的关系知,\[x_{1}+x_{2}=\dfrac{2k^{2}+4}{k^{2}}, x_{1}x_{2}=1,\]于是\[\begin{split}|AC|&=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\\&=\sqrt{1+k^{2}}\sqrt{(x_{1}+x_{2})^{2}-4x_{1}x_{2}}\\&=\sqrt{1+k^{2}}\sqrt{\left(\dfrac{2k^{2}+4}{k^{2}}\right)^{2}-4}\\&=\dfrac{4(1+k^{2})}{k^{2}}.\end{split}\]又因为 $AC\perp BD$,所以直线 $BD$ 的斜率为 $-\dfrac{1}{k}$,从而直线 $BD$ 的方程为$$y=-\dfrac{1}{k}(x-1).$$同理可求得$$|BD|=4(1+k^{2}).$$故\[\begin{split}S_{ABCD}&=\dfrac{1}{2}\cdot |AC|\cdot |BD|\\&=\dfrac{8(1+k^{2})^{2}}{k^{2}}\\&=8\left(k^{2}+\dfrac{1}{k^{2}}+2\right)\\&\geqslant 8\cdot (2+2)\\&=32,\end{split}\]当 $k=\pm 1$ 时等号成立.
因此四边形 $ABCD$ 的最小面积为 $32$.
答案
解析
备注