已知椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 右焦点为 $F$,右准线 $l$ 交 $x$ 轴于点 $N$,过椭圆上一点 $P$ 作 $PM$ 垂直于准线 $l$,垂足为 $M$.若 $PN$ 平分 $\angle FPM$,且四边形 $OFMP$ 为平行四边形,证明 $e>\dfrac23$.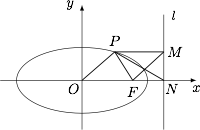

【难度】
【出处】
2012年全国高中数学联赛江苏省复赛(一试)
【标注】
【答案】
略
【解析】
因为$$\angle NPM=\angle NPF , \angle NPM=\angle NPF,$$所以 $\angle NPF=\angle PNF$,得 $PF=NF$.
又四边形 $OFMP$ 为平行四边形,所以 $PM=OF$,且 $\dfrac{PF}{PM}=e$,于是$$e=\dfrac{PF}{PM}=\dfrac{NF}{OF}=\dfrac{ON-OF}{OF}=\dfrac{1}{e^2}-1,$$从而 $e^3+e^2=1$.
因为函数 $f(t)=t^3+t^2$ 在 $t>0$ 时,单调递增,且$$f\left(\dfrac23\right)=\dfrac{8}{27}+\dfrac49=\dfrac{20}{27}<1=f(e),$$所以 $e>\dfrac23$,故结论成立.
又四边形 $OFMP$ 为平行四边形,所以 $PM=OF$,且 $\dfrac{PF}{PM}=e$,于是$$e=\dfrac{PF}{PM}=\dfrac{NF}{OF}=\dfrac{ON-OF}{OF}=\dfrac{1}{e^2}-1,$$从而 $e^3+e^2=1$.
因为函数 $f(t)=t^3+t^2$ 在 $t>0$ 时,单调递增,且$$f\left(\dfrac23\right)=\dfrac{8}{27}+\dfrac49=\dfrac{20}{27}<1=f(e),$$所以 $e>\dfrac23$,故结论成立.
答案
解析
备注