如图，$PA,PB$ 为圆 $O$ 的两条切线，切点分别为 $A,B$，过点 $P$ 的直线交圆 $O$ 于 $C,D$ 两点，交弦 $AB$ 于点 $Q$．求证：$PQ^2=PC\cdot PD-QC\cdot QD$．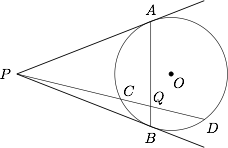
【难度】
【出处】
2009年全国高中数学联赛陕西省预赛（二试）
【标注】
【答案】
略
【解析】
如图，连结 $OP$ 交 $AB$ 于点 $H$，则 $OP\perp AB$．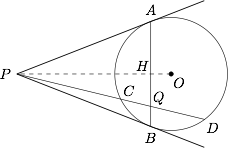
因为\[\begin{split}PA^2-PQ^2&=(PH^2+AH^2)-(PH^2+HQ^2)\\&=(AH+HQ)(AH-HQ)\\&=AQ\cdot QB,\end{split}\]所以$$PQ^2=PA^2-AQ\cdot QB.$$由切割线定理及相交弦定理，得$$PA^2=PC\cdot PD , AQ\cdot QB=QC\cdot QD,$$故$$PQ^2=PC\cdot PD-QC\cdot QD.$$
因为\[\begin{split}PA^2-PQ^2&=(PH^2+AH^2)-(PH^2+HQ^2)\\&=(AH+HQ)(AH-HQ)\\&=AQ\cdot QB,\end{split}\]所以$$PQ^2=PA^2-AQ\cdot QB.$$由切割线定理及相交弦定理，得$$PA^2=PC\cdot PD , AQ\cdot QB=QC\cdot QD,$$故$$PQ^2=PC\cdot PD-QC\cdot QD.$$
答案
解析
备注
