如图，$\odot O$ 与线段 $AB$ 相切于点 $M$，与以 $AB$ 为直径的半圆相切于点 $E$．$CD\perp AB$ 于点 $D$，$CD$ 与以 $AB$ 为直径的半圆交于点 $C$，且与 $\odot O$ 相切于点 $F$，连结 $AC,CM$．求证：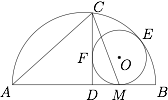
【难度】
【出处】
2009年全国高中数学联赛福建省预赛
【标注】
-
$A,F,E$ 三点共线；标注答案略解析如图，设 $AB$ 中点为 $P$．
由条件知 $\odot P$ 与 $\odot O$ 内切于 $E$，故 $P,O,E$ 三点共线．
连结 $FO$，由 $CD\perp AB$，$CD$ 切 $\odot O$ 于点 $F$，知$$CD\perp OF , FO\parallel AP , \angle{EOF}=\angle{EPA}.$$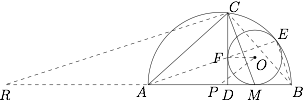
因为$$OE=OF , PE=PA,$$所以 $\angle{OEF}=\angle{PEA}$，$A,F,E$ 三点共线． -
$AC=AM$；标注答案略解析在 $\odot O$ 中，由切割线定理知$$AM^2=AF\cdot AE.$$连结 $EB$，由于 $AE\perp EB$，因此 $E,F,D,B$ 四点共圆，所以$$AD\cdot AB=AF\cdot AE.$$连结 $BC$，则 $AC\perp CB$，因此$$AC^2=AD\cdot AB=AF\cdot AE=AM^2,$$故 $AC=AM$．
-
$MC^2=2MD\cdot MA$．标注答案略解析延长 $MA$ 至点 $R$，使得 $AR=AM$．
连结 $CR$，由 $(2)$ 中 $AC=AM$ 知，$RC\perp CM$，所以$$MC^2=MD\cdot MR=2MD\cdot MA.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
