如图，已知点 $O$ 为凸四边形 $ABCD$ 内的一点，$AO=OB$，$CO=OD$，$\angle AOB=\angle COD=120^\circ$，点 $E,F,G$ 分别是线段 $AB,BC,CD$ 的中点．求证：$\triangle EFG$ 为正三角形．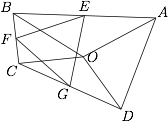
【难度】
【出处】
2008年全国高中数学联赛江苏省复赛（二试）
【标注】
【答案】
略
【解析】
在 $\triangle AOC$ 与 $\triangle BOD$ 中，$$OA=OB,OC=OD,\angle AOC=\angle BOD,$$所以 $\triangle AOC\cong \triangle BOD$，因此$$AC=BD , \angle OAC=\angle OBD.$$设 $AC$ 分别交 $BD,BO$ 于点 $P,Q$．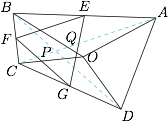
因为$$\angle DPA=\angle OBD+\angle PQB=\angle OAC+\angle OQA=60^\circ,$$所以$$\angle GFE=\angle DPA=60^\circ,$$又 $EF=FG$，因此 $\triangle EFG$ 为正三角形．
因为$$\angle DPA=\angle OBD+\angle PQB=\angle OAC+\angle OQA=60^\circ,$$所以$$\angle GFE=\angle DPA=60^\circ,$$又 $EF=FG$，因此 $\triangle EFG$ 为正三角形．
答案
解析
备注
