如图，正方体 $ABCD - A_1 B_1 C_1 D_1$ 的棱长为 $ 2 $，动点 $ E,F $ 在棱 $ A _ 1 B _ 1 $ 上．点 $ Q $ 是棱 $ CD $ 的中点，动点 $ P $ 在棱 $ AD $ 上，若 $ EF=1 $，$ DP=x $，${ A _ 1 } E=y$（$ x,y $ 大于零），则三棱锥 $ P-EFQ $ 的体积 \((\qquad)\) 
【难度】
【出处】
2010年高考北京卷（文）
【标注】
【答案】
C
【解析】
延长 $QP$ 与 $BA$ 交于点 $R$，如图．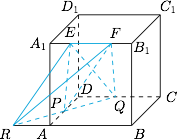
根据题意，四面体 $PEFQ$ 的体积$$V_{P-EFQ}=\dfrac{RP}{RQ}\cdot V_{R-EFQ}=\dfrac{RP}{RQ}\cdot V_{Q-EFR}=\dfrac{AP}{AD}\cdot V_{Q-EFR},$$而 $\triangle REF$ 的面积及 $Q$ 到平面 $EFR$ 的距离均为定值，因此四面体 $PEFQ$ 的体积只与 $P$ 点的位置有关．
根据题意，四面体 $PEFQ$ 的体积$$V_{P-EFQ}=\dfrac{RP}{RQ}\cdot V_{R-EFQ}=\dfrac{RP}{RQ}\cdot V_{Q-EFR}=\dfrac{AP}{AD}\cdot V_{Q-EFR},$$而 $\triangle REF$ 的面积及 $Q$ 到平面 $EFR$ 的距离均为定值，因此四面体 $PEFQ$ 的体积只与 $P$ 点的位置有关．
题目
答案
解析
备注
