已知数列 $\{a_n\}$ 满足条件 $a_{n+1}=-\dfrac{(a_n+1)^2}{a_n+2}$，首项 $a_1=-\dfrac 12$，求 $\lim\limits_{n\to \infty}a_n$．
【难度】
【出处】
无
【标注】
【答案】
$-1+\dfrac{\sqrt 2}2$
【解析】
递推公式对应的不动点为 $x=-1\pm\dfrac{\sqrt 2}2$，于是有\[\begin{aligned} a_{n+1}+1-\dfrac{\sqrt 2}2&=-\dfrac{\left(a_n+1-\dfrac{\sqrt 2}2\right)\left(a_n+\sqrt 2\right)}{a_n+2},\\ a_{n+1}+1+\dfrac{\sqrt 2}2&=-\dfrac{\left(a_n+1+\dfrac{\sqrt 2}2\right)\left(a_n-\sqrt 2\right)}{a_n+2},\end{aligned}\]迭代函数$$f(x)=-\dfrac {(x+1)^2}{x+2}=-\left[(x+2)+\dfrac 1{x+2}\right]+2,$$在 $(-1,+\infty)$ 上单调递减，容易证明\[-\dfrac 12\leqslant a_n\leqslant -\dfrac 16,\]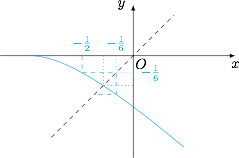
于是\[\left|-\dfrac{a_n+\sqrt 2}{a_n+2}\right|<\dfrac{2\sqrt 2-1}3<1,\]因此\[\lim\limits_{n\to \infty}a_n=-1+\dfrac{\sqrt 2}2.\]
于是\[\left|-\dfrac{a_n+\sqrt 2}{a_n+2}\right|<\dfrac{2\sqrt 2-1}3<1,\]因此\[\lim\limits_{n\to \infty}a_n=-1+\dfrac{\sqrt 2}2.\]
答案
解析
备注
